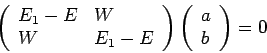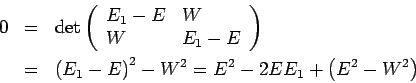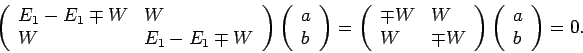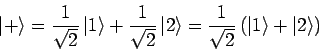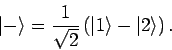Next: Rechenbeispiel 1: 2 -Funktionen.
Up: Entartung/Quasientartung
Previous: Entartung/Quasientartung
Contents
Betrachten wir ein zweifach entartetes Energieniveau, dessen Entartung in der 1. Ordnung
der Störungstheorie nicht aufgehoben wird:
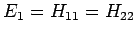 und 2 dazugehörige Wellenfunktionen
und 2 dazugehörige Wellenfunktionen
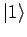 und
und
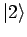 . Alle anderen Zustände des Spektrums liegen energetisch weit
entfernt. Die Wellenfunktionen der 2 ''gestörten''
Zustände
. Alle anderen Zustände des Spektrums liegen energetisch weit
entfernt. Die Wellenfunktionen der 2 ''gestörten''
Zustände
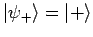 und
und
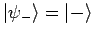 sind dann
sind dann
Die Säkulargleichung für solche Systeme lautet
mit 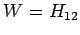 (als reell angenommen). Aus der Bedingung
(als reell angenommen). Aus der Bedingung
erhalten wir
Die Koeffizienten 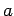 ,
, 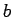 sind dann durch die Ls'gen des folgenden
Gleichungssystems gegeben:
sind dann durch die Ls'gen des folgenden
Gleichungssystems gegeben:
Für die entsprechenden Werte bekommen wir entweder
oder
d.h.
und
Die Wellenfunktionen müssen normiert sein, so dass
Da diese Koeffizienten stets reell gewählt werden können, bekommen
wir
und
Die erste WF ist symmetrisch gegenüber des Austauschens der
Teilchen, die zweite ist antisymmetrisch.




Next: Rechenbeispiel 1: 2 -Funktionen.
Up: Entartung/Quasientartung
Previous: Entartung/Quasientartung
Contents
Prof. Igor Sokolov
2005-02-14
![]() und 2 dazugehörige Wellenfunktionen
und 2 dazugehörige Wellenfunktionen
![]() und
und
![]() . Alle anderen Zustände des Spektrums liegen energetisch weit
entfernt. Die Wellenfunktionen der 2 ''gestörten''
Zustände
. Alle anderen Zustände des Spektrums liegen energetisch weit
entfernt. Die Wellenfunktionen der 2 ''gestörten''
Zustände
![]() und
und
![]() sind dann
sind dann