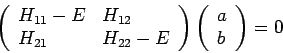Next: Beispiel: eine zweifach einartetes
Up: Störungstheorie in stationären Zuständen
Previous: Noch ein Zugang
Contents
Betrachten wir zunächst eine einfache Situation mit zwei behachbarnten
Niveaus. Die Beiträge aller anderen Niveaus in der Störungsrechnung
sind klein, und können auf den bekannten Wegen bestimmt oder
vollständig vernachlässigt werden. Wir bekommen dann die Situation
für ein effektives Zweiniveausystem (2-dimensionaler Hilbertraum
in der Energiedarstellung mit Zuständen
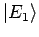 und
und
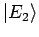 ). In diesem Fall
). In diesem Fall
Die Säkulardeterminante lautet dann
und ergibt die Energiewerte
Die gleiche Formel gilt auch für entartete Zustände:
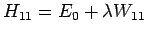 ,
,
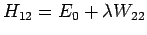 . Da die
Matrixelementen der Störung normalerweise nicht verschwinden, wird die
Entartung durch die Störung aufgehoben.
. Da die
Matrixelementen der Störung normalerweise nicht verschwinden, wird die
Entartung durch die Störung aufgehoben.
Betrachten wir den Grenzfall
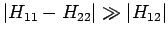 . Entwicklung der Wurzel ergibt z.B. für
. Entwicklung der Wurzel ergibt z.B. für 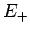
Vernachlässigen wir in 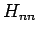 (mit
(mit 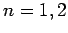 )
)
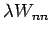 in Vergleich mit
in Vergleich mit 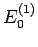 so erhalten wir unsere übliche Formel
für die Störungsrechnung 2 Ordnung, wobei die
Beiträge entfernter Niveaus vernachlässigt sind.
so erhalten wir unsere übliche Formel
für die Störungsrechnung 2 Ordnung, wobei die
Beiträge entfernter Niveaus vernachlässigt sind.
Nachdem 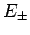 bekannt sind, kann man aus dem Gleichungssystem
bekannt sind, kann man aus dem Gleichungssystem
auch die Entwicklungskoeffizienten 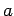 und
und 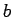 finden (beachte Normierung!).
Die gleichen Überlegungen gelten i.A. auch für die höheren
Entartungsgrade. Man erhält die Säkularmatrizen höherer Ordnung.
finden (beachte Normierung!).
Die gleichen Überlegungen gelten i.A. auch für die höheren
Entartungsgrade. Man erhält die Säkularmatrizen höherer Ordnung.
Subsections




Next: Beispiel: eine zweifach einartetes
Up: Störungstheorie in stationären Zuständen
Previous: Noch ein Zugang
Contents
Prof. Igor Sokolov
2005-02-14
![]() und
und
![]() ). In diesem Fall
). In diesem Fall
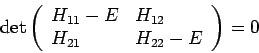
![\begin{displaymath}
E_{\pm }=\frac{1}{2}\left[ H_{11}+H_{22}\pm \sqrt{\left(
H_{...
...{22}\right) ^{2}+4\left\vert H_{12}\right\vert ^{2}}\right] .
\end{displaymath}](img1935.png)
![]() . Entwicklung der Wurzel ergibt z.B. für
. Entwicklung der Wurzel ergibt z.B. für ![]()
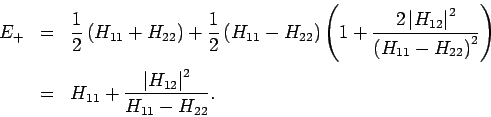
![]() bekannt sind, kann man aus dem Gleichungssystem
bekannt sind, kann man aus dem Gleichungssystem