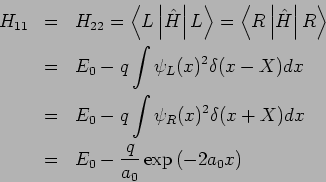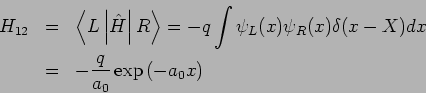Next: Rechenbeispiel 2: Abschätzung der
Up: Entartung/Quasientartung
Previous: Beispiel: eine zweifach einartetes
Contents
Im experimentellen Teil der Vorlesung hat man normalerweise die
Störung als Einflüß des schwachen äußeren Feldes betrachtet.
Wir können aber die theoretische Möglichkeit der ''Einschaltung''
der Wechselwirkung ausnutzen um Störungstheorie auch in der Situationen anzuwenden,
bei denen es am Anfang nicht klar ist was diese ''Störung'' eigentlich bedeutet.
Dies ist sehr einfach zu verstehen, wenn man die WF'nen z.B. für das
Potential aus 2 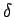 -funktionen
-funktionen
betrachtet; 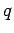 ist die Potentialstärke. Wenn die 2
ist die Potentialstärke. Wenn die 2 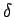 -Mulden
weit voneinender entfernt sind, können wir die 2 gleichwertigen
Zustände unterscheiden: ''Elektron in der linke Mulde'' (
-Mulden
weit voneinender entfernt sind, können wir die 2 gleichwertigen
Zustände unterscheiden: ''Elektron in der linke Mulde'' (
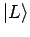 ) und ''Elektron in der rechte Mulde'' (
) und ''Elektron in der rechte Mulde'' (
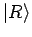 ). Da die Mulden weit voneinender entfernt sind, mischen
sich die Zustände nicht. Das Elektron bleibt da, wo es von Anfang an
(nach der Präparation des Systems) war. Die Zustände
). Da die Mulden weit voneinender entfernt sind, mischen
sich die Zustände nicht. Das Elektron bleibt da, wo es von Anfang an
(nach der Präparation des Systems) war. Die Zustände
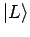 und
und
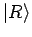 mit WF
mit WF
und
(mit
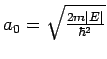 der
Lokalizationslänge des Zustands; die Energie beider Zuständen
der
Lokalizationslänge des Zustands; die Energie beider Zuständen
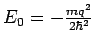 ) sind zueinender orthogonal weil für
) sind zueinender orthogonal weil für
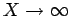 gilt
gilt
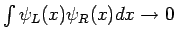 .
Die Wechselwirkung zwischen der Zuständen wird eingeschaltet, wenn wir
jetzt
.
Die Wechselwirkung zwischen der Zuständen wird eingeschaltet, wenn wir
jetzt 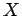 verkleinern. Die nichtdiagonalen Elemente der
Säkulardeterminante sind jetzt
verkleinern. Die nichtdiagonalen Elemente der
Säkulardeterminante sind jetzt
(die Entartung wird in der 1. Ordnung nicht aufgehoben) und
(man hat auch
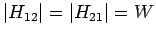 ). Man sieht dass bei größeren
Abständen
). Man sieht dass bei größeren
Abständen 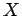 die diagonale ''Störung''
die diagonale ''Störung'' 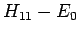 im Vergleich
mit dem nichtdiagonalen Element vernachlässigt werden kann (das ist die
speziale Eigenschaft der stark lokalisierten
im Vergleich
mit dem nichtdiagonalen Element vernachlässigt werden kann (das ist die
speziale Eigenschaft der stark lokalisierten 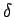 -Potential). Die
Energien der gestörten Zustände sind dann
-Potential). Die
Energien der gestörten Zustände sind dann
und
(vergleichen Sie das Resultat mit ihrer exakten Lösung aus einer
Hausaufgabe!).




Next: Rechenbeispiel 2: Abschätzung der
Up: Entartung/Quasientartung
Previous: Beispiel: eine zweifach einartetes
Contents
Prof. Igor Sokolov
2005-02-14
![]() -funktionen
-funktionen
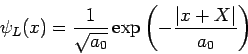
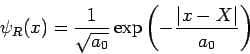
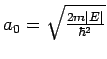 der
Lokalizationslänge des Zustands; die Energie beider Zuständen
der
Lokalizationslänge des Zustands; die Energie beider Zuständen