



Next: Identische Teilchen
Up: Tensorprodukt zweier Vektorräume
Previous: Tensorprodukt zweier Vektorräume
Contents
Betrachten wir zunächst die Situation mit unterschiedlichen Teilchen.
Seien 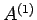 und
und 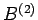 die Observablen in den Räumen
die Observablen in den Räumen 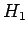 und
und 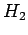 ,
, 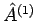 und
und 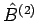 sind die entsprechende
Hermite'schen Operatoren die nur auf die Funktionen von entsprechenden
Variablen (z.B. von
sind die entsprechende
Hermite'schen Operatoren die nur auf die Funktionen von entsprechenden
Variablen (z.B. von
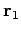 bzw.
bzw.
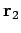 in
Ortsdarstellun) wirken. Als Observablen in
in
Ortsdarstellun) wirken. Als Observablen in 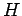 betrachtet man i.A. die
Operatorfunktionen von
betrachtet man i.A. die
Operatorfunktionen von 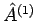 und
und 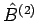 :
:
(typischerweise allg. Potenzreihen). In der Basis der Produktzustände
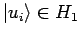 ,
,
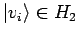 gilt:
gilt:
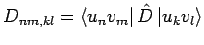 ist das Matrixelement von
ist das Matrixelement von 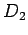 bezüglich
der Basis
bezüglich
der Basis
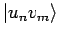 . Das Indexpaar
. Das Indexpaar 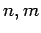 numeriert
die Zeilen, das Indexpaar
numeriert
die Zeilen, das Indexpaar 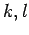 numeriert die Spalten (Beispiel später).
Die Einwirkung des Operators
numeriert die Spalten (Beispiel später).
Die Einwirkung des Operators 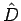 auf den Zustand
auf den Zustand
wird durch den Zustand
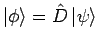
gegeben, mit den Entwicklungskoeffizienten
Die Operatoren 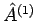 und
und 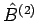 wirken nur in einem der
beiden Teilräume
wirken nur in einem der
beiden Teilräume 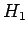 oder
oder 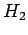 . Die sind also die Produkte
. Die sind also die Produkte
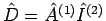 oder
oder
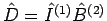 . Die
entsprechenden Wirkungen sind:
. Die
entsprechenden Wirkungen sind:
und
Daher folgt:
und somit
Die Operatoren, die auf verschiedene (unterscheidbare) Teilchen wirken,
kommutieren.
Der Hilbertraum 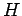 ist ein passender Hilbertraum auch in dem Fall, wenn die
Teilchen wechselwirken. In diesem Fall kann man schreiben
ist ein passender Hilbertraum auch in dem Fall, wenn die
Teilchen wechselwirken. In diesem Fall kann man schreiben
mit 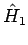 und
und 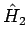 - Einteilchen-Hamiltonoperatoren, und
- Einteilchen-Hamiltonoperatoren, und
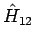 - Wechselwirkung. Die EF von
- Wechselwirkung. Die EF von 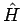 können dann über
die Basis der Produktfunktionen entwickelt werden.
können dann über
die Basis der Produktfunktionen entwickelt werden.
Falls man mehr als 2 unterscheidbare Teilchen hat, bildet man einen
Hilbertraum
und benutzt das Basis der entsprechenden Produktzustände.




Next: Identische Teilchen
Up: Tensorprodukt zweier Vektorräume
Previous: Tensorprodukt zweier Vektorräume
Contents
Prof. Igor Sokolov
2005-02-14
![]() und
und ![]() die Observablen in den Räumen
die Observablen in den Räumen ![]() und
und ![]() ,
, ![]() und
und ![]() sind die entsprechende
Hermite'schen Operatoren die nur auf die Funktionen von entsprechenden
Variablen (z.B. von
sind die entsprechende
Hermite'schen Operatoren die nur auf die Funktionen von entsprechenden
Variablen (z.B. von
![]() bzw.
bzw.
![]() in
Ortsdarstellun) wirken. Als Observablen in
in
Ortsdarstellun) wirken. Als Observablen in ![]() betrachtet man i.A. die
Operatorfunktionen von
betrachtet man i.A. die
Operatorfunktionen von ![]() und
und ![]() :
:
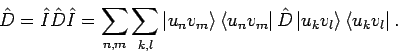

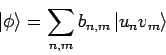
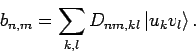
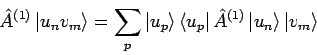
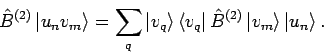
![]() ist ein passender Hilbertraum auch in dem Fall, wenn die
Teilchen wechselwirken. In diesem Fall kann man schreiben
ist ein passender Hilbertraum auch in dem Fall, wenn die
Teilchen wechselwirken. In diesem Fall kann man schreiben