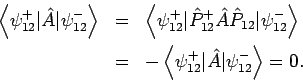Next: Symmetrische und antisymmetrische Wellenfunktionen
Up: Vielteilchensysteme I
Previous: Observablen im Produktraum
Contents
Aus den Versuchen zur Erklärung der Atomstrukturen in Rahmen von ''älteren'' Quantentheorien hat man gelernt, dass die stationären Niveaus
nicht durch beliebeg vielen Hüllenelektronen besetzt werden können.
In Rahmen der ''neueren'' Theorie ist diese Beobachtung eine Folge des
Pauli-Prinzips, dass 2 Elektronen nie gleichzeitig ein und denselben
Zustand besetzen können. D.h. dass auch 2 nicht wechselwirkende (oder
sehr schwach wechselwirkende) Elektronen nicht ganz voneinander unabhängig sein können. Hier handelt es sich um eine Folge der prinzipiellen Ununterscheidbarkeit identischer Teilchen.
Da Teilchen ununterscheidbar sind, kann man nicht zwischen den Situationen
unterscheiden ''Teilchen 1 am Ort
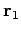 , Teilchen 2 am Ort
, Teilchen 2 am Ort
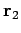 '' und ''Teilchen 2 am Ort
'' und ''Teilchen 2 am Ort
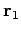 , Teilchen 1 am
Ort
, Teilchen 1 am
Ort
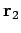 '': da die Teilchen keine Individualität besitzen,
entsprechen diese einer experimentellen Situation: Ein Teilchen am Ort
'': da die Teilchen keine Individualität besitzen,
entsprechen diese einer experimentellen Situation: Ein Teilchen am Ort
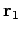 , ein Teilchen am Ort
, ein Teilchen am Ort
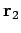 .
.
Der 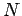 -Teilchenzustand ist daher ein ''Pauschalzustand'': Jede
Fragestellung, die auf Beobachtung eines Einzehlteilchens abzieht ist
sinnlos. Es kommen nur solche Observablen in Betracht, die explizit von den
Koordinaten aller Teilchen in ''symmetrischer'' Weise abhängen. Da die
Produkte der Eintelichenzustände einen Hilbertraum bilden, kann man
annehmen, dass die
-Teilchenzustand ist daher ein ''Pauschalzustand'': Jede
Fragestellung, die auf Beobachtung eines Einzehlteilchens abzieht ist
sinnlos. Es kommen nur solche Observablen in Betracht, die explizit von den
Koordinaten aller Teilchen in ''symmetrischer'' Weise abhängen. Da die
Produkte der Eintelichenzustände einen Hilbertraum bilden, kann man
annehmen, dass die 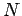 -Teilchen-Zustände
-Teilchen-Zustände
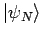 die spezielle Linearkombinationen von
die spezielle Linearkombinationen von
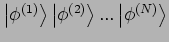 sind
(der obere Index numeriert die Teilchen).
sind
(der obere Index numeriert die Teilchen).
Sind alle Teilchen des Systems gleichartig, dann bleibt der
Hamilton-Operator dieses Systems 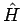 bei Vertauschung eines beliebigen
Teilchenpaares unverändert. Bezeichnen wir den Operator solcher
Vertauschung der Teilchen
bei Vertauschung eines beliebigen
Teilchenpaares unverändert. Bezeichnen wir den Operator solcher
Vertauschung der Teilchen 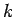 und
und 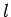
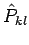 (das Transpositionsoperator):
(das Transpositionsoperator):
Wegen der Ununterscheidbarkeit soll der Operator 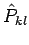 nicht die
Norm der WF verändern.
nicht die
Norm der WF verändern. 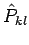 ist deswegen unitär:
ist deswegen unitär:
Dieser Operator soll mit dem Hamiltonian kommutieren
und die Eigenwerte von 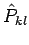 sind die Bewegungsintegrale. Die
Eigenvektoren von
sind die Bewegungsintegrale. Die
Eigenvektoren von 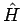 sind demnach auch solche von
sind demnach auch solche von 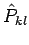 . Die
verschiedene Transpositionoperatoren
. Die
verschiedene Transpositionoperatoren 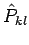 und
und 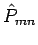 sind
i.A. nicht vertauschbar.
sind
i.A. nicht vertauschbar.
Zweimalige Anwendung von 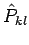 führt zu dem Ausgangszustand zurück:
führt zu dem Ausgangszustand zurück:
d.h.
Daher gilt
d.h. der Operator 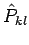 ist Hermitesch.
ist Hermitesch.
Betrachten wir zuerst das System aus nur 2 Teilchen, und betrachten wir die
Eigenfunktionen von 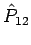 :
:
Es gilt
und andererseits
Daher
und da 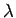 reell (
reell (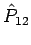 Hermitesch!) gibt es nur 2 Möglichkeiten:
Hermitesch!) gibt es nur 2 Möglichkeiten:
Die Eigenfunktionen zum Eigenwert 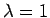 heißen symmetrische
Funktionen,
heißen symmetrische
Funktionen,
die EF zu 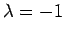 heißen antisymmetrische Funktionen
heißen antisymmetrische Funktionen
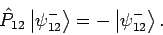
Da der Eigenwert von 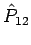 ein Bewegungsintegral ist bleibt die
Symmetrieeigenschaft der WF zeitlich unverändert.
ein Bewegungsintegral ist bleibt die
Symmetrieeigenschaft der WF zeitlich unverändert.
- In Mehrteilchensystemen (
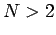 ) sind nur die WF erlaubt die entweder
symmetrisch oder antisymmetrisch bezüglich der Vertauschung jedes Teilchenpaars sind.
) sind nur die WF erlaubt die entweder
symmetrisch oder antisymmetrisch bezüglich der Vertauschung jedes Teilchenpaars sind.
- Jeder Operator der ''vernünftigen'' Observablen soll mit
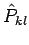 kommutieren (experimentelle Ununterscheidbarkeit). Alle
Matrizenelemente sollen nach der durch
kommutieren (experimentelle Ununterscheidbarkeit). Alle
Matrizenelemente sollen nach der durch 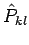 definierten unitären Transformation erhalten bleiben:
definierten unitären Transformation erhalten bleiben:
- Symmetrische und antisymmetrische Zustände sind zueinender
orthogonal:
(da
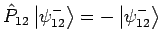 und
und
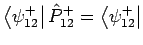 ).
).
- Es gibt keine Observablen, die einen symmetrischen Zustand auf einen
antisymmetrischen Zustand (und umgekehrt) abbilden können:
- Die Zustände eines bestimmten Systems identischer Teilchen gehören sämtlich zu dem Hilbert-(Unter)raum der Symmetrischen Zustände
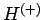 oder zum Hilbert-(Unter)raum der antisymmetrische Zustände
oder zum Hilbert-(Unter)raum der antisymmetrische Zustände 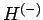 : könnte das System sowohl symmetrische als auch
antisymmetrische Zustände haben, sollten auch ihre Linearkombinationen
als zulässige Zustände erlaubt sein. Die sind aber weder symmetrisch
noch antisymmetrisch.
: könnte das System sowohl symmetrische als auch
antisymmetrische Zustände haben, sollten auch ihre Linearkombinationen
als zulässige Zustände erlaubt sein. Die sind aber weder symmetrisch
noch antisymmetrisch.
- Die symmetrischen WF bestimmen die Systeme aus Bosonen
(Photonen, Helium-Atome, u.s.w.; i.A. die Teichen mit Gesamtspin 0,
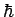 ,
, 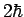 , u.s.w.). Die antisymmetrische FWF entsprechen den Fermionen
(Elektronen, Protonen, Neutronen, Neutrinos, ..., mit Spin
, u.s.w.). Die antisymmetrische FWF entsprechen den Fermionen
(Elektronen, Protonen, Neutronen, Neutrinos, ..., mit Spin
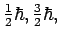 ...).
...).




Next: Symmetrische und antisymmetrische Wellenfunktionen
Up: Vielteilchensysteme I
Previous: Observablen im Produktraum
Contents
Prof. Igor Sokolov
2005-02-14
![]() , Teilchen 2 am Ort
, Teilchen 2 am Ort
![]() '' und ''Teilchen 2 am Ort
'' und ''Teilchen 2 am Ort
![]() , Teilchen 1 am
Ort
, Teilchen 1 am
Ort
![]() '': da die Teilchen keine Individualität besitzen,
entsprechen diese einer experimentellen Situation: Ein Teilchen am Ort
'': da die Teilchen keine Individualität besitzen,
entsprechen diese einer experimentellen Situation: Ein Teilchen am Ort
![]() , ein Teilchen am Ort
, ein Teilchen am Ort
![]() .
.
![]() -Teilchenzustand ist daher ein ''Pauschalzustand'': Jede
Fragestellung, die auf Beobachtung eines Einzehlteilchens abzieht ist
sinnlos. Es kommen nur solche Observablen in Betracht, die explizit von den
Koordinaten aller Teilchen in ''symmetrischer'' Weise abhängen. Da die
Produkte der Eintelichenzustände einen Hilbertraum bilden, kann man
annehmen, dass die
-Teilchenzustand ist daher ein ''Pauschalzustand'': Jede
Fragestellung, die auf Beobachtung eines Einzehlteilchens abzieht ist
sinnlos. Es kommen nur solche Observablen in Betracht, die explizit von den
Koordinaten aller Teilchen in ''symmetrischer'' Weise abhängen. Da die
Produkte der Eintelichenzustände einen Hilbertraum bilden, kann man
annehmen, dass die ![]() -Teilchen-Zustände
-Teilchen-Zustände
![]() die spezielle Linearkombinationen von
die spezielle Linearkombinationen von
![]() sind
(der obere Index numeriert die Teilchen).
sind
(der obere Index numeriert die Teilchen).
![]() bei Vertauschung eines beliebigen
Teilchenpaares unverändert. Bezeichnen wir den Operator solcher
Vertauschung der Teilchen
bei Vertauschung eines beliebigen
Teilchenpaares unverändert. Bezeichnen wir den Operator solcher
Vertauschung der Teilchen ![]() und
und ![]()
![]() (das Transpositionsoperator):
(das Transpositionsoperator):
![]() führt zu dem Ausgangszustand zurück:
führt zu dem Ausgangszustand zurück:
![]() :
: