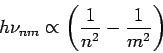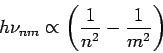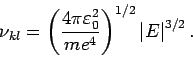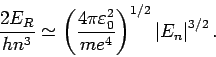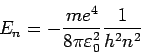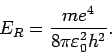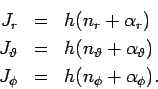Next: Sommerfeld'sche Phasenquantisierung und die
Up: Das Korrespondenzprinzip
Previous: Das Korrespondenzprinzip
Contents
Wasserstoffatom. Es ist experimentell bekannt, dass
ist, die Proportionalitätskonstante 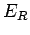 ist zunächst unbekannt.
Wir wissen aber, dass ein klassisches Elektron, das mit der Frequenz
ist zunächst unbekannt.
Wir wissen aber, dass ein klassisches Elektron, das mit der Frequenz 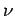 sich bewegt, vor allem mit der Frequenz
sich bewegt, vor allem mit der Frequenz 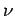 abstrahlt (Elektrodynamik!).
D.h.
abstrahlt (Elektrodynamik!).
D.h.
und
(Oberschwingungen). Es gilt also
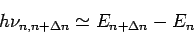 |
(6) |
oder
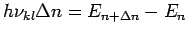 .
.
- Berechnung der Rydberg-Konstante. Aus der Bahlmer-Gl. in Quantenfall
bekommt man
so dass
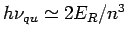 . Im klassischen Fall
. Im klassischen Fall
Für
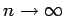 soll
soll
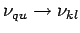 stimmen, also gilt
stimmen, also gilt
Daher
und
- die HASENOEHRL'sche Quantenbedingung. Aus Gl.(6) folgt:
Die Integration der Gleichung ergibt
mit Integrationskonstante 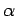 . Diese kann nicht aus der Korrespondenzprinzip
bestimmt werden, und muss dem experimentellen Befund angepasst werden.
. Diese kann nicht aus der Korrespondenzprinzip
bestimmt werden, und muss dem experimentellen Befund angepasst werden.
- Die SOMMERFELD'sche Phasenquantisierung. Da
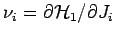 bekommt man
bekommt man
(Vgl. Gl.(5): Für die Eigenwirkungsvariables ist 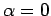 ).
Für das Kepler-Problem
).
Für das Kepler-Problem
Die Hauptquantenzahl
(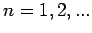 ) definiert die Energie (wenn man
) definiert die Energie (wenn man
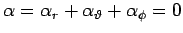 wählt). Die Bewegung ist entartet, da
wählt). Die Bewegung ist entartet, da 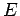 nur durch
nur durch 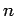 definiert ist (klassisch: nur von der großen Halbachse
der Orbits bestimmt). Die anderen Quantenzahlen sind
definiert ist (klassisch: nur von der großen Halbachse
der Orbits bestimmt). Die anderen Quantenzahlen sind
(Nebenquantenzahl),
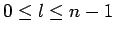 und
und
(die magnetische Quantenzahl),
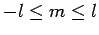 .
.




Next: Sommerfeld'sche Phasenquantisierung und die
Up: Das Korrespondenzprinzip
Previous: Das Korrespondenzprinzip
Contents
Prof. Igor Sokolov
2005-02-14