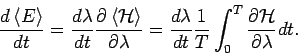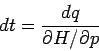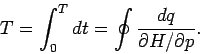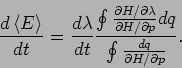Next: Die Materiewellen
Up: Das Korrespondenzprinzip
Previous: Anwendungsbeispiel:
Contents
Die Ideen von Bohr und Sommerfeld werden klarer, wenn wir ihren Hintergrund
erläutern. Die Eigenzustände eines Quantensystems sind sehr
langlebig auf mikroskopischen Skalen (trotz ihre Wechselwirkung mit der
Umgebung ändern sich ihre Energien und folglich ihre Bewegungsperioden 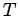 zwischen der ''Quantensprüngen'' nicht). Diese Tatsache soll anhand des
Korrespondenzprinzips eine klassische Entsprechung haben.
zwischen der ''Quantensprüngen'' nicht). Diese Tatsache soll anhand des
Korrespondenzprinzips eine klassische Entsprechung haben.
Nehmen wir an, dass die Hamilton-Fkt. des Systems von einem Parameter 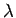 abhängt. Dieser Parameter ändert sich langsam (''adiabatisch'') unter Einfluß äußerer Ursachen, so dass
abhängt. Dieser Parameter ändert sich langsam (''adiabatisch'') unter Einfluß äußerer Ursachen, so dass
In solchen Fällen existiert ein Wert (Kombination aus 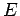 und
und 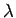 ) der sich kaum verändert (praktisch konstant bleibt). Solche
Kombinationen nennt man adiabatische Invarianten. Nur solche
''langsamen'' Variablen können ''gequantelt'' werden.
) der sich kaum verändert (praktisch konstant bleibt). Solche
Kombinationen nennt man adiabatische Invarianten. Nur solche
''langsamen'' Variablen können ''gequantelt'' werden.
Eindimensionale Beispiel: Hamilton-Fkt.:
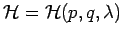 .
.
Mittlung über die Periode:
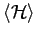 - über die Periode gemittelte
Wert von
- über die Periode gemittelte
Wert von 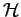 bei
bei
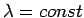 . Aus
. Aus
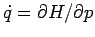 ergibt sich
ergibt sich
und daher
Es gilt:
Wir sehen jetzt 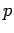 als die Funktion
als die Funktion
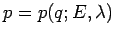 an. Da
an. Da
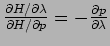 (Jacobi-Determinant!) und
(Jacobi-Determinant!) und
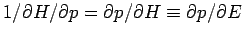 , es ergibt sich
, es ergibt sich
Diese Gl. hat die Form
mit
(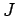 ist zeitabhängig durch
ist zeitabhängig durch 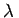 und
und 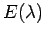 ). Das ist
genau unsere Wirkungsvariable!
). Das ist
genau unsere Wirkungsvariable!




Next: Die Materiewellen
Up: Das Korrespondenzprinzip
Previous: Anwendungsbeispiel:
Contents
Prof. Igor Sokolov
2005-02-14
![]() zwischen der ''Quantensprüngen'' nicht). Diese Tatsache soll anhand des
Korrespondenzprinzips eine klassische Entsprechung haben.
zwischen der ''Quantensprüngen'' nicht). Diese Tatsache soll anhand des
Korrespondenzprinzips eine klassische Entsprechung haben.
![]() abhängt. Dieser Parameter ändert sich langsam (''adiabatisch'') unter Einfluß äußerer Ursachen, so dass
abhängt. Dieser Parameter ändert sich langsam (''adiabatisch'') unter Einfluß äußerer Ursachen, so dass
![]() .
.