



Next: Erklärung der Quantisierungspostulate
Up: Die Materiewellen
Previous: Die Materiewellen
Contents
Einfachste Welle: Ebene Welle
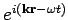 : eine Schwingung
breitet sich aus in der Richtung von Wellenvektor
: eine Schwingung
breitet sich aus in der Richtung von Wellenvektor 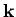 mit der
(Phasen-)geschwindigkeit
mit der
(Phasen-)geschwindigkeit
Da jede Welle als Superposition von ebenen Wellen aufgefasst werden kann,
genügt die Kenntniss von dem Dispersionsgesetz 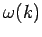 für die
Beschreibung der zeitlichen Entwicklung.
für die
Beschreibung der zeitlichen Entwicklung.
Allg.: das Wellenpaket (Superposition) ist gegeben durch
oder (ab hier, einfachheitshalbe, 1D)
Nehmen wir an, die Fkt. 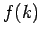 ist groß im
ist groß im 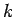 -Bereich von der
Breite
-Bereich von der
Breite 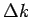 um irgendeinen Wert
um irgendeinen Wert 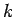 . Die Gruppengeschwindigket
. Die Gruppengeschwindigket
ist mit der Teilchengeschw. im klassischen Limes gleichgesetzt. Da diese gleich
ist, bekommen wir
In allen Dimensionen
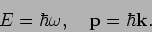 |
(7) |
Diese Zusammenhänge gelten auch relativistisch.
Diese Wellen sind reell! Beugungsexperimente:
- Elektronenbeugung:
- Davisson & Germer (1927) - Monokristalle, von Laue-Beugung
- G.P. Thomson (1928) Polykristalline Körper, Debye-Scherer-Bild
- Beugung von monoenergetischen Strahlen von He und H
 , Stern
(1932).
, Stern
(1932).
- Neutronenbeugung (Neutronen müßen erst entdekt werden!).
In einem nicht-relativistischen Fall in sich langsam änderndem Potential
(1d) ist
oder
Subsections




Next: Erklärung der Quantisierungspostulate
Up: Die Materiewellen
Previous: Die Materiewellen
Contents
Prof. Igor Sokolov
2005-02-14
![]() : eine Schwingung
breitet sich aus in der Richtung von Wellenvektor
: eine Schwingung
breitet sich aus in der Richtung von Wellenvektor ![]() mit der
(Phasen-)geschwindigkeit
mit der
(Phasen-)geschwindigkeit
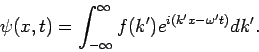
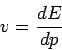
![\begin{displaymath}
\lambda =\frac{h}{p}=\frac{h}{\sqrt{2m\left[ E-U(r)\right] }}.
\end{displaymath}](img238.png)