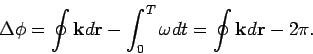Next: ''Wellengleichung'' für die Materiewellen:
Up: Das freie Wellenpaket.
Previous: Das freie Wellenpaket.
Contents
Die Gl.(7) gibt die Möglichkeit,  in jedem Punkt
der Orbits zu bestimmen. Bei jeder Umdrehung der Teilchen wächst die
Phase um
in jedem Punkt
der Orbits zu bestimmen. Bei jeder Umdrehung der Teilchen wächst die
Phase um
Damit das Wellenbild stationär ist, soll gelten
Daher
So lassen sich alle Bohr-Sommerfeld'sche Regeln begründen. Die
stationären Zustände gleichen der stehenden Wellen in einem
Resonator.
Prof. Igor Sokolov
2005-02-14
![]() in jedem Punkt
der Orbits zu bestimmen. Bei jeder Umdrehung der Teilchen wächst die
Phase um
in jedem Punkt
der Orbits zu bestimmen. Bei jeder Umdrehung der Teilchen wächst die
Phase um