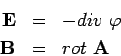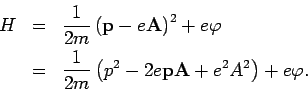Next: Vorsichtsmaßnamen
Up: Schrödinger-Gleichung: Das Kochrezept.
Previous: Schrödinger-Gleichung: Das Kochrezept.
Contents
Klassische Bewegungsgleichungen:
Die Felder 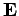 und
und 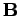 sind durch
sind durch
gegeben. Die Lagrange-Funktion lautet
Daher ist die Hamilton-Funktion
Die Korrespondenzregel
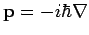 und die Symmetrisierung
des Glieds
und die Symmetrisierung
des Glieds  ergibt:
ergibt:
Prof. Igor Sokolov
2005-02-14