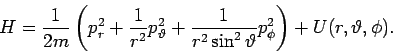Vorsichtsmaßnamen

• In der klassichen Mechanik sind die verallgemeinerten Koordinaten $q$ (und daher die entsprechenden Impulse) in gewissem Sinne willkürlich. Z.B. kann man $H$ in kartesischen Koordinaten schreiben als
  

  $$H=\frac{1}{2m}\left( p_{x}^{2}+p_{y}^{2}+p_{z}^{2}\right) +U(x,y,z)$$ (8)

  
  
  oder in Kugelkoordinaten
  

  $$H=\frac{1}{2m}\left( p_{r}^{2}+\frac{1}{r^{2}}p_{\vartheta }... ...in ^{2}\vartheta }p_{\phi }^{2}\right) +U(r,\vartheta ,\phi ).$$ (9)

  
  
  Die Benutzung der Korrespondenzregel im 1. Fall ergibt
  
  $$\hat{H}=\frac{-\hbar ^{2}}{2m}\Delta +U(x,y,z).$$
  
  
  Dann können wir (wenn wir wollen) den Laplacian in Kugelkoordinaten überführen:
  
  $$\hat{H}=\frac{-\hbar ^{2}}{2m}\left[ \frac{1}{r^{2}}\frac{\p... ...2}}{\partial \phi ^{2}}\right) \right] +U(r,\vartheta ,\phi ).$$
  
  
  Diese Form ist richtig. Wenn wir dagegen unsere Vorschrift unmittelbar auf die Gl.(9) anwenden, erhalten wir eine andere Gleichung
  
  $$\hat{H}=\frac{-\hbar ^{2}}{2m}\left[ \frac{\partial ^{2}}{% ... ...tial ^{2}}{\partial \phi ^{2}} \right] +U(r,\vartheta ,\phi ).$$
  
  
  Diese Gleichung ist falsch!

• Einschübe. Z.B. haben wir in einem eindimensionalen Problem klassisch die kinetischen Energie
  
  $$T=\frac{p^{2}}{2m},$$
  
  
  die sich nicht ändert, wenn wir, z.B. schreiben
  
  $$T_1=\frac{1}{2m}\frac{1}{\sqrt{f(x)}}pf(x)p\frac{1}{\sqrt{f(x)}}.$$
  
  
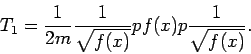
  Die eintsprechenden Operatoren sind dagegen unterschiedlich:
  
  $$\hat{T}_{1}=-\frac{\hbar ^{2}}{2m}\frac{\partial ^{2}}{\partial x^{2}}$$
  
  
  und
  
  $$\hat{T}_{1}=-\frac{\hbar ^{2}}{2m}\left( \frac{\partial ^{2}... ...\prime \prime } }{2f}+\frac{(f^{\prime })^{2}}{4f^{2}}\right)$$
  
  
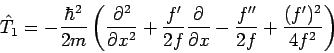
  vor Symmetrisierung (wegen der Nicht-Kommutativität der Koordinate und des Impulses). Diese Form ist auch nach der Symmetrisierung falsch!

  $\Rightarrow$ Für ''richtige'' Teilchen in Euklid'schen Raum ist die einfachste Form (keine Einschübe!) zu benutzen.

Die Erklärung der beiden Tatsachen hat mit der Wahrscheinlichkeitsinterpretation der Wellenfunktion zu tun.