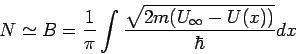Betrachten wir zunächst die Energie ![]() (den Fall
(den Fall ![]() werden
wir später betrachten; man kann auch zeigen (gleiche Methode wie hier!),
dass es keine Zustände gibt mit
werden
wir später betrachten; man kann auch zeigen (gleiche Methode wie hier!),
dass es keine Zustände gibt mit ![]() ). In diesem Fall für
). In diesem Fall für ![]() (und für
(und für ![]() ) hat man
) hat man ![]() und für
und für
![]() hat man
hat man ![]() .
.
Teillösungen: Ab hier
![]()
Für
![]() hat man
hat man
![]() (sonnst ist
(sonnst ist ![]() nicht integrabel). Daher ist die einzige Lsg links von
der Mulde
nicht integrabel). Daher ist die einzige Lsg links von
der Mulde
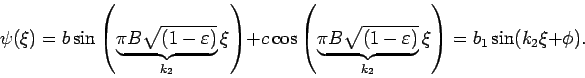
Das ''Zusammennähen'': die Fkt. und ihre Ableitung sind am Orten ![]() und
und ![]() stetig.
stetig.
Die Kontinuitätsbedingungen für die Funktion und für ihre
Ableitung. Trick: da ![]() und
und
![]() stetig sind, und da an
stetig sind, und da an
![]()
![]() ist (kann man nachträglich nachprüfen),
sollen die logarithmische Ableitungen
ist (kann man nachträglich nachprüfen),
sollen die logarithmische Ableitungen
![]() an beiden Seiten der
Potentialsprünge gleich sein. Daher:
an beiden Seiten der
Potentialsprünge gleich sein. Daher:
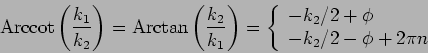

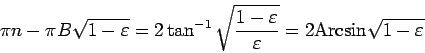
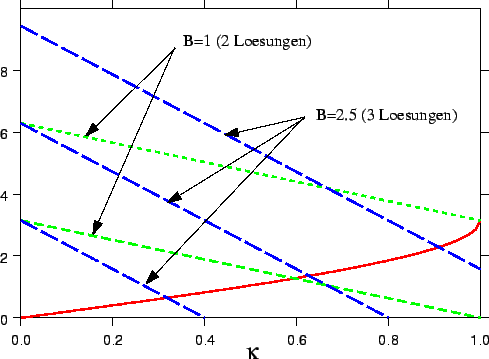
Das heißt:
![]()