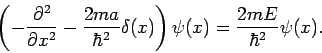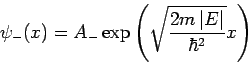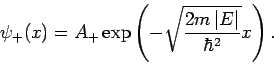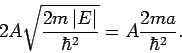Next: Die Parität der Zustände
Up: Beispiel: Das Rechteckpotential.
Previous: Gebundene Zustände.
Contents
Betrachten wir jetzt genauer den Spezialfall
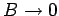 , mit nur einem
gebundenen Zustand. In diesem Fall existiert nur eine Lösung der Gl.
, mit nur einem
gebundenen Zustand. In diesem Fall existiert nur eine Lösung der Gl.
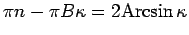 (siehe Bild) mit
(siehe Bild) mit
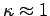 .
Da in diesem Fall
.
Da in diesem Fall
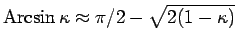 ,
bekommen wir
,
bekommen wir
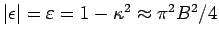 . In
natürlichen Einheiten erhalten wir
. In
natürlichen Einheiten erhalten wir
Dieses Resultat stimmt in allen Fällen wenn
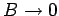 , d.h. in einem
sehr tiefen aber schmalen Topf, sovie in einem Topf, der breit, aber flach ist.
, d.h. in einem
sehr tiefen aber schmalen Topf, sovie in einem Topf, der breit, aber flach ist.
Betrachten wir nochmals den Grenzfall
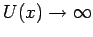 ,
,
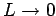 ,
aber
,
aber 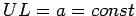 . In diesem Fall haben wir
. In diesem Fall haben wir
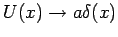 .
Die Schrödinger-Gl. lautet:
.
Die Schrödinger-Gl. lautet:
Links und rechts von dem 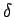 -Potential haben wir die Lösungen
-Potential haben wir die Lösungen
und
Die Wellenfunktion ist stetig, d.h.
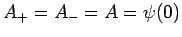 . Die
Integration der beiden Seiten der Gl. zwischen
. Die
Integration der beiden Seiten der Gl. zwischen 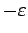 und
und 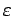 ergibt
ergibt
Die Ableitung von 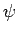 erfährt in
erfährt in 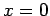 einen endlichen Sprung, d.h.
einen endlichen Sprung, d.h.
Daher ist die Energie des gebundenen Zustands




Next: Die Parität der Zustände
Up: Beispiel: Das Rechteckpotential.
Previous: Gebundene Zustände.
Contents
Prof. Igor Sokolov
2005-02-14
![]() , mit nur einem
gebundenen Zustand. In diesem Fall existiert nur eine Lösung der Gl.
, mit nur einem
gebundenen Zustand. In diesem Fall existiert nur eine Lösung der Gl.
![]() (siehe Bild) mit
(siehe Bild) mit
![]() .
Da in diesem Fall
.
Da in diesem Fall
![]() ,
bekommen wir
,
bekommen wir
![]() . In
natürlichen Einheiten erhalten wir
. In
natürlichen Einheiten erhalten wir
![]() ,
,
![]() ,
aber
,
aber ![]() . In diesem Fall haben wir
. In diesem Fall haben wir
![]() .
Die Schrödinger-Gl. lautet:
.
Die Schrödinger-Gl. lautet: