



Next: Gebundene Zustände.
Up: Stationäre Zustände
Previous: Stationäre Zustände
Contents
Die stationäre Schrödinger-Gl. ist
mit Parametern: Längenskala 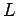 , Energieskala
, Energieskala 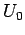 . Dimensionslose
Länge
. Dimensionslose
Länge 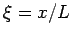 , dimensionslose Energie
, dimensionslose Energie
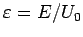 ,
,
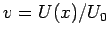 .
.
Der dimensionslose Parameter
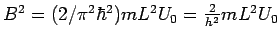 (d.h.
(d.h.
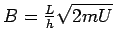 ) wird der
BORN'sche Parameter genannt. Die SGl. lässt sich daher in
der folgenden Form schreiben:
) wird der
BORN'sche Parameter genannt. Die SGl. lässt sich daher in
der folgenden Form schreiben:
![\begin{displaymath}
\psi ^{\prime \prime }+\pi ^{2}B^{2}\left[ \epsilon -v(\xi )\right] \psi =0
\end{displaymath}](img333.png) |
(10) |
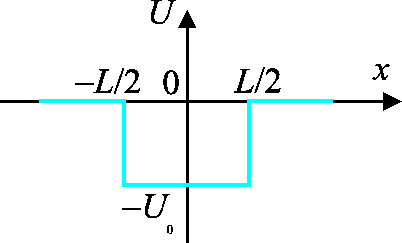
Der Potentialtopf 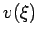 hat eine Breite 1 und Tiefe 1, d.h. das
Potential
hat eine Breite 1 und Tiefe 1, d.h. das
Potential 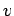 nimmt nur 2 Werte an: entweder
nimmt nur 2 Werte an: entweder 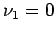 , oder
, oder 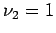 .
.
Die Gl.(10) ist eine Sturm-Liouville-Gl. Wir suchen ihre
kontinuierlichen, differenzierbaren Ls'gen in
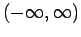 . In unserem
Fall ist sie eine Gl. mit stückweise-konstanten Parametern. Allg. Ls'gen:
. In unserem
Fall ist sie eine Gl. mit stückweise-konstanten Parametern. Allg. Ls'gen:
Die Gesamtlösung wird aus 3 Teile (links von der, in der Mulde,
rechts von der Mulde) zusammengestellt, mit Hilfe den
Kontinuitätsbedingungen für 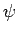 und
und
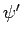 .
.
Subsections
Prof. Igor Sokolov
2005-02-14

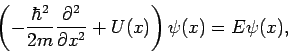
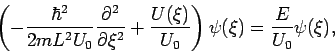
![]() . In unserem
Fall ist sie eine Gl. mit stückweise-konstanten Parametern. Allg. Ls'gen:
. In unserem
Fall ist sie eine Gl. mit stückweise-konstanten Parametern. Allg. Ls'gen:
![]() und
und
![]() .
.