Sei ![]() eine Lösung der SGl zur Energie
eine Lösung der SGl zur Energie ![]() und
und
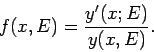
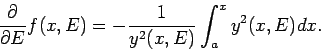
Beweis: Die Lsg. ![]() ist gegeben, wenn die Werte
ist gegeben, wenn die Werte ![]() und
und
![]() in irgendeinem Punkt
in irgendeinem Punkt ![]() gegeben sind. Für den Wert
der Energie
gegeben sind. Für den Wert
der Energie ![]() bekommen wir eine andere Lösung,
bekommen wir eine andere Lösung,
![]() . Aus Wronskian-Theorem folgt:
. Aus Wronskian-Theorem folgt:
![\begin{displaymath}
\left. W(y,y+\delta y)\right\vert _{a}^{x}=-\frac{2m}{\hbar ^{2}}\delta
E\int_{a}^{x}y(x)[y(x)+\delta y(x)]dx.
\end{displaymath}](img511.png)
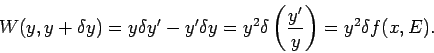
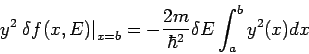
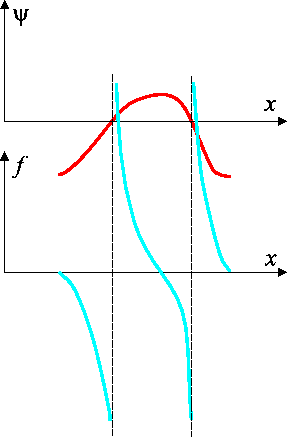
Bemerkung 1:
![]() ist stets negativ, und
divergiert an Knotenpunkten von
ist stets negativ, und
divergiert an Knotenpunkten von ![]() . Daher ist
. Daher ist ![]() eine monotone
Funktion. Das Betrag von
eine monotone
Funktion. Das Betrag von ![]() wächst mit
wächst mit ![]() links von der Nullstelle und
wird kleiner mit
links von der Nullstelle und
wird kleiner mit ![]() rechts von der Nullstelle.
rechts von der Nullstelle.
Bemerkung 2: Man kann
![]() nehmen und die Funktionen
betrachten, die samt ihrer Ableitung für
nehmen und die Funktionen
betrachten, die samt ihrer Ableitung für
![]() verschwinden.
verschwinden.