



Next: Streuzustände (kontinuierliches Spektrum)
Up: Stationäre Zustände
Previous: Die Logarithmische Ableitung der
Contents
Die entsprechende dimensionslose Schrödingergl. lautet
mit
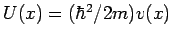 und
und
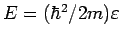 .
Betrachten wir das Potential
.
Betrachten wir das Potential 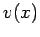 mit
mit
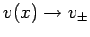 für
für
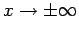 . Die Werte
. Die Werte 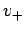 und
und 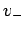 teilen die
Energieskala in 3 Gebiete (wir nehmen an z.B. dass
teilen die
Energieskala in 3 Gebiete (wir nehmen an z.B. dass 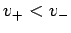 ):
):




Next: Streuzustände (kontinuierliches Spektrum)
Up: Stationäre Zustände
Previous: Die Logarithmische Ableitung der
Contents
Prof. Igor Sokolov
2005-02-14
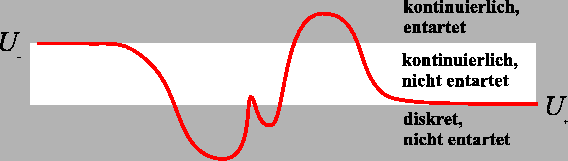
![]() . Das Spektrum ist daher diskret und nicht entartet.
. Das Spektrum ist daher diskret und nicht entartet.