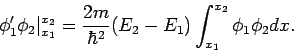Next: Die Logarithmische Ableitung der
Up: Stationäre Zustände
Previous: Wahrscheinlichkeitsstrom und Erhalten der
Contents
erlaubt allgemeine Aussagen über die Lsg. der eindimensionalen
Schrödinger-Gl. Seien 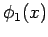 und
und 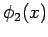 zwei reelle
Lsgen der stationären Schrödinger-Gl. zu den Energien
zwei reelle
Lsgen der stationären Schrödinger-Gl. zu den Energien 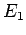 und
und 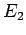 . Multiplizieren wir die entsprechenge Gl'en
. Multiplizieren wir die entsprechenge Gl'en
und
mal 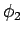 (
(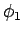 ) und bilden die Differenz:
) und bilden die Differenz:
Man integriert die Gl. zwichen 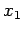 und
und 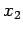 (
(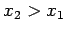 ), und
wendet die partielle Integration an:
), und
wendet die partielle Integration an:
oder
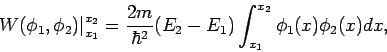 |
(11) |
mit
die Wronski-Determinante (Wronskian). Die Gl.(11) hat viele
wichtige Folgen.
- Für
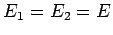 ist
ist
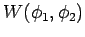 . Haben die
Lösungen eine gemeinsame Nullstelle,
. Haben die
Lösungen eine gemeinsame Nullstelle,
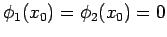 ,
so ist
,
so ist 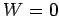 . Daher
. Daher
so dass die Ls'gen zueinander proportional sind. Wenn sie als normiert
vorausgesetzt sind, so ist
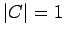 und
und
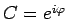 . Der
Zustand
. Der
Zustand 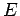 ist nicht entartet.
ist nicht entartet.
- Die Lösungen sind dann und nur dann auf dem Interval
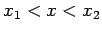 linear abhängig, wenn das Wronskian dort identisch
verschwindet.
linear abhängig, wenn das Wronskian dort identisch
verschwindet.
- Seien
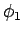 und
und 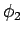 die Ls'gen von SGl mit
unterschiedlichen Eigenwerten
die Ls'gen von SGl mit
unterschiedlichen Eigenwerten 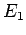 und
und 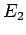 aus diskretem Spektrum
(d.h. normierbar). Dann sind die Ls'gen
aus diskretem Spektrum
(d.h. normierbar). Dann sind die Ls'gen 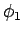 und
und 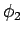 ortogonal, d.h.
ortogonal, d.h.
Bew.: Die normierbaren Ls'gen sind diejenige mit
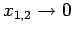 für
für
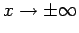 . Daher gilt
. Daher gilt
Bemerkung: Wenn die Ls'gen nicht reell sind, gilt i.A.
Die Ls'gen der SGl. mit Hermite'schen 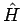 bilden ein orthonormiertes System. Diese Aussage gilt auch in höheren
Dimensionen.
bilden ein orthonormiertes System. Diese Aussage gilt auch in höheren
Dimensionen.
- Seien
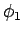 und
und 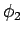 zwei reelle Eigenfunktionen mit
zwei reelle Eigenfunktionen mit 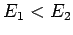 . Wir zeigen jetzt, dass zwischen 2 Knoten (Nullstellen) der
Funktion
. Wir zeigen jetzt, dass zwischen 2 Knoten (Nullstellen) der
Funktion 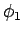 mindestens ein Knoten der Funktion
mindestens ein Knoten der Funktion 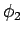 liegt.
liegt.
Seien 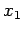 und
und 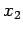 zwei aufeinenderfolgende Nullpunkte von
zwei aufeinenderfolgende Nullpunkte von 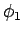 . Betrachten wir die Wronski-Determinante zwischen diesen Punkten. Es gilt:
. Betrachten wir die Wronski-Determinante zwischen diesen Punkten. Es gilt:
Zwischen den Punkten 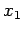 und
und 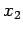 ändert die Fkt.
ändert die Fkt. 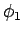 nicht ihre Vorzeichen, z.B. ist
nicht ihre Vorzeichen, z.B. ist 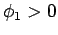 . Daher ist
. Daher ist
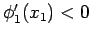 und
und
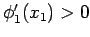 . Nehmen wir an, dass die
Funktion
. Nehmen wir an, dass die
Funktion 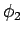 auf dem Intervall ihre Vorzeichen nicht ändert.
Damit ist die linke Seite der Gleichung negativ, und ihre rechte Seite
positiv, was zu einem Widerspruch führt. Daher muss
auf dem Intervall ihre Vorzeichen nicht ändert.
Damit ist die linke Seite der Gleichung negativ, und ihre rechte Seite
positiv, was zu einem Widerspruch führt. Daher muss 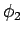 auf dem
Intervall
auf dem
Intervall 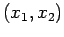 ihr Vorzeichen ändern.
ihr Vorzeichen ändern.
Man kann die Eigenfunktionen nach Anzahl ihrer Knotenpunkten ordnen und einen
folgenden Satz beweisen:
- Das Oszillationstheorem (der Knotensatz). Besitzt der
eindimensionale Hamiltonian ein diskretes Spektrum mit Energien
so hat die Wellefunktion 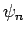 genau
genau 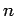 Nullstellen (Knoten).
Nullstellen (Knoten).
Subsections




Next: Die Logarithmische Ableitung der
Up: Stationäre Zustände
Previous: Wahrscheinlichkeitsstrom und Erhalten der
Contents
Prof. Igor Sokolov
2005-02-14
![]() und
und ![]() zwei reelle
Lsgen der stationären Schrödinger-Gl. zu den Energien
zwei reelle
Lsgen der stationären Schrödinger-Gl. zu den Energien ![]() und
und ![]() . Multiplizieren wir die entsprechenge Gl'en
. Multiplizieren wir die entsprechenge Gl'en
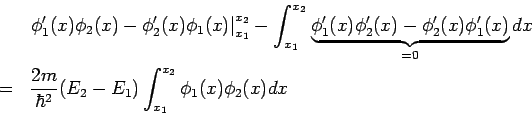
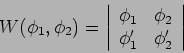
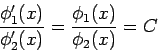
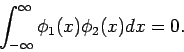
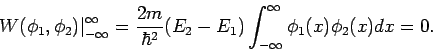
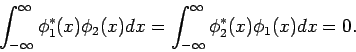
![]() und
und ![]() zwei aufeinenderfolgende Nullpunkte von
zwei aufeinenderfolgende Nullpunkte von ![]() . Betrachten wir die Wronski-Determinante zwischen diesen Punkten. Es gilt:
. Betrachten wir die Wronski-Determinante zwischen diesen Punkten. Es gilt: