



Next: Beispiel: Das Rechteckpotential.
Up: Quantenmechanik I WS 04/05
Previous: Vorsichtsmaßnamen
Contents
In einem konservativen System ist 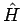 (und damit seine Energie)
zeitunabhängig. Damit hat die Lösung
(und damit seine Energie)
zeitunabhängig. Damit hat die Lösung 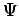 eine
wohldefinierte Frequenz
eine
wohldefinierte Frequenz 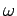 , so dass
, so dass
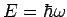 . Es
gilt also:
. Es
gilt also:
Wenn wir diesen Ausdruck in der Schrödinger-Gl. einsetzen, bekommen
wir
Diese Gl. wird als stationäre Schrödinger-Gl. bezeichnet, und
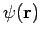 wird als WF des stationären Zustands bezeichnet (obwohl sie
keine richtige WF ist, da es an der Zeitabhängigkeit fehlt!).
wird als WF des stationären Zustands bezeichnet (obwohl sie
keine richtige WF ist, da es an der Zeitabhängigkeit fehlt!).
Diskutieren wir zunächst die Eigenschaften der SGl für ein Teilchen
in einem skalaren Potential 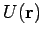 . Es wird angenommen
. Es wird angenommen
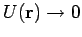 für
für
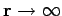 .
.
Das Problem,
die (physikalisch vernünftigen) Lösungen von der Gl.
zu finden ist das Eigenwertproblem.
Um das Problem vollständig zu definieren, muß man die Randbedingungen
und die Regularitätseigenscheften der WF festlegen.
Subsections




Next: Beispiel: Das Rechteckpotential.
Up: Quantenmechanik I WS 04/05
Previous: Vorsichtsmaßnamen
Contents
Prof. Igor Sokolov
2005-02-14
![]() (und damit seine Energie)
zeitunabhängig. Damit hat die Lösung
(und damit seine Energie)
zeitunabhängig. Damit hat die Lösung ![]() eine
wohldefinierte Frequenz
eine
wohldefinierte Frequenz ![]() , so dass
, so dass
![]() . Es
gilt also:
. Es
gilt also:
![]() . Es wird angenommen
. Es wird angenommen
![]() für
für
![]() .
.
![\begin{displaymath}
\hat{H}\psi (\mathbf{r})=\left[ -\frac{\hbar ^{2}}{2m}\Delta +U(\mathbf{r}%
)\right] \psi (\mathbf{r})=E\psi (\mathbf{r})
\end{displaymath}](img319.png)