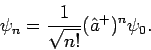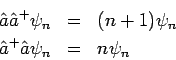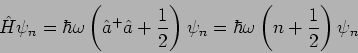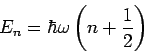Next: Multidimensionaler harmonischer Oszillator
Up: Stationäre Zustände
Previous: Kronig-Penney-Modell
Contents
Alles, was schwingt, kann mehr oder weniger durch eine harmonischen
Oszillation angenähert werden!
mit
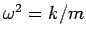 ,
, 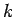 -Federkonstante. Bemerkung: da
-Federkonstante. Bemerkung: da
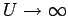 für
für
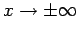 , besitzt das Operator nur
diskretes Spektrum.
, besitzt das Operator nur
diskretes Spektrum.
SGl:
Variablenwechsel: Dimensionslose Koordinate 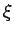 und Energie
und Energie 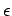 :
:
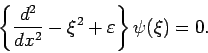 |
(12) |
Da für
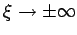
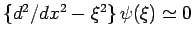 , ist für grosse
, ist für grosse 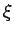
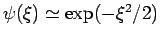 . Daher sucht man die Lsg. in der Form:
. Daher sucht man die Lsg. in der Form:
Einstellen in Eq.(12) ergibt für 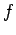 :
:
Damit die Lsg. von (12) überall endlich bleibt, muss 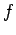 nicht
besonders schnell wachsend sein (z.B. ein Polynom). Solche Ls'gen existieren
tatsächlich für
nicht
besonders schnell wachsend sein (z.B. ein Polynom). Solche Ls'gen existieren
tatsächlich für
mit 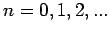 :
:
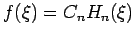 ,
, 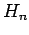 - ein HERMITE-Polynom:
- ein HERMITE-Polynom:
Die Hermite-Polynome genügen folgenden Rekursionsbeziehungen:
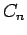 ist eine Normierungskonstante:
ist eine Normierungskonstante:
Daher:
(
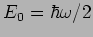 - die Nullpunktenergie).
- die Nullpunktenergie).
Wie kommt man auf die Lösungen? Suchen wir nach einer Lösung der Gl.(5.7) in Form einer Potenzreihe:
(da die Lösungen der Ausgangsgleichung eine wohldefinierte Parität
haben müßen, bestehen die Reihen ausschlisslich aus geraden oder aus
ungeraden Potenzen von 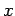 ). Einstellen in der Gl.(5.7) und sammeln der
Koeffizienten vor den gleichen Potenzen von
). Einstellen in der Gl.(5.7) und sammeln der
Koeffizienten vor den gleichen Potenzen von 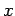 ergibt:
ergibt:
Da 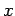 eine freie Variable ist, soll der Ausdruck
eine freie Variable ist, soll der Ausdruck ![$[...]$](img738.png) für jedes
Glied verschwinden. Daraus resultiert eine Rekursionsformel:
für jedes
Glied verschwinden. Daraus resultiert eine Rekursionsformel:
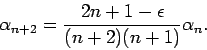 |
(13) |
Die erlaubt das Ausdrucken von allen Koeffizienten durch 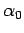 für die gerade und durch
für die gerade und durch 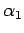 für die ungerade Lösungen.
Ist ein der Koeffizienten
für die ungerade Lösungen.
Ist ein der Koeffizienten 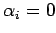 so verschwinden auch alle folgende
Koeffizienten: Die Reihe bricht ab.
so verschwinden auch alle folgende
Koeffizienten: Die Reihe bricht ab.
Wenn die Reihe nicht abbricht, dann haben wir für große 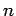
d.h.
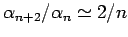 . Das entspricht für große
. Das entspricht für große 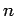 der Reihenentwicklung von
der Reihenentwicklung von
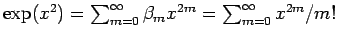 mit
mit
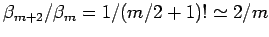 für die geraden Zustände oder der
Reihenentwicklung von
für die geraden Zustände oder der
Reihenentwicklung von 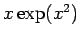 für die ungeraden Zustände
(gleichermassen). Das heißt, dass wenn die Reihe nicht abbricht, divergiert
die Wellenfunktion
für die ungeraden Zustände
(gleichermassen). Das heißt, dass wenn die Reihe nicht abbricht, divergiert
die Wellenfunktion
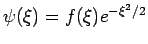 für
für
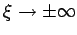 . Die Reihe muss also abbrechen. Das ist nur dann
möglich, wenn
. Die Reihe muss also abbrechen. Das ist nur dann
möglich, wenn
wohin unsere Energiebedingung folgt. Die Hermite-Polynome folgen aus unserer
Rekursionsformel Eq.(13) und der
Normierungsbedingung für die gesamte Wellenfunktion.
Mathematischer Einschub: Die Orthogonalpolynome
Das System der Polynome
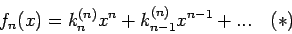 |
(14) |
wird als eine Familie der Ortogonalpolynome auf
![$\left[ a,b\right] $](img753.png) bezeichnet, wenn sie der (gewichteten) Orthogonalitätsbeziehung
bezeichnet, wenn sie der (gewichteten) Orthogonalitätsbeziehung
für eine Gewichtung 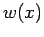 und
und 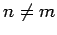 genügen. Der obere Index in
Gl. (*) bezeichnet das Glied der Familie, der untere Index entspricht der
Potenz von
genügen. Der obere Index in
Gl. (*) bezeichnet das Glied der Familie, der untere Index entspricht der
Potenz von 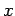 . Die Normierung ist durch eine Zusatzbeziehung gegeben
. Die Normierung ist durch eine Zusatzbeziehung gegeben
Solche Polynome genügen einer Rekursionsbeziehung
mit
Alle solche Polynome folgen aus der RODRIGUES-Formul
wobei das Polynom 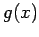 unabhängig von
unabhängig von 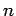 ist (das gewährleistet
die Orthogonalität, Gl.(*)), und genügt einer Differenzialgleichung
ist (das gewährleistet
die Orthogonalität, Gl.(*)), und genügt einer Differenzialgleichung
wobei die Polynome 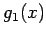 und
und 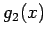 nicht von
nicht von 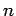 abhängen. Die
Hermite-Polynome sind eine Familie mit
abhängen. Die
Hermite-Polynome sind eine Familie mit 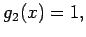
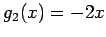 und
und
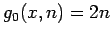 , die Gewichtung
, die Gewichtung
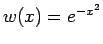 , und
, und
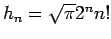 . Für solche Polynome gilt
. Für solche Polynome gilt
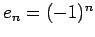 und
und 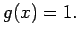 Alle
Eigenschaften der Orthogonalpolynome finden ihre Entsprechung in Eigenschaften
der Erzeugungs- und Vernichtungsoperatoren.
Alle
Eigenschaften der Orthogonalpolynome finden ihre Entsprechung in Eigenschaften
der Erzeugungs- und Vernichtungsoperatoren.
Aus der Rekursionsbedingungen für die Hermite-Polynome folgt:
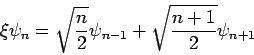 |
(15) |
und
und somit
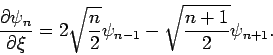 |
(16) |
Aus der (15) und (16) folgen nützliche Beziehungen:
Die entsprechende Operatoren
und
werden das Vernichtungs- und Erzeugungsoperator genannt. In
Ausgangsvariablen des Problems sind
und
Aus dem Kommutator
![$\left[ \hat{x},\hat{p}\right] =i\hbar $](img784.png) bekommt man
bekommt man
(die Operatoren 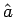 und
und 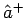 sind dimensionslos). Da gilt
sind dimensionslos). Da gilt
und
bekommt unser Hamiltonian
die Gestalt
Die Kombiantion
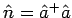 wird als Besetzungszahloperator bezeichet.
wird als Besetzungszahloperator bezeichet.
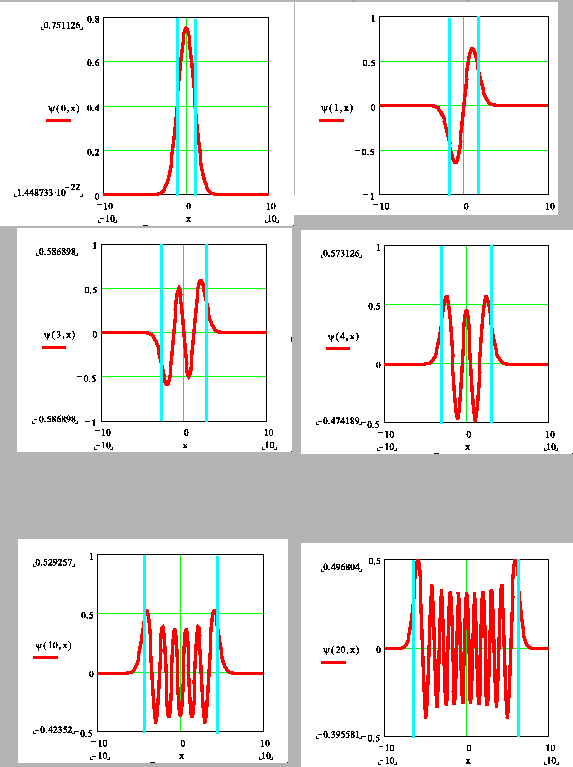
Die Wellenfunktion des 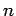 -ten Zustandes kan man durch wiederhohlte
Anwendung des Operators
-ten Zustandes kan man durch wiederhohlte
Anwendung des Operators 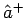 auf
auf
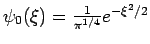 bestimmen:
bestimmen:
Durch wiederholte Anwendung von (17) bekommt man die Gleichungen
aus denen ebenfalls
![$\left[ \hat{a},\hat{a}^{+}\right] =1$](img795.png) folgt. Für
die Eigenfunktion
folgt. Für
die Eigenfunktion 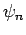 gilt dann
gilt dann
woraus man sofort
ablesen kann.
Subsections




Next: Multidimensionaler harmonischer Oszillator
Up: Stationäre Zustände
Previous: Kronig-Penney-Modell
Contents
Prof. Igor Sokolov
2005-02-14
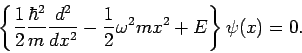
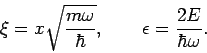
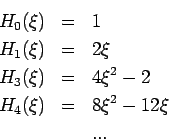
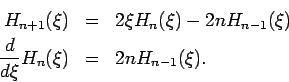
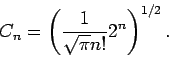
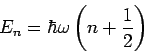
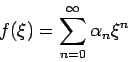
![\begin{displaymath}
\sum_{n}\left[ \alpha _{n+2}(n+2)(n+1)+\alpha _{n}(\epsilon -1-2n)\right]
x^{n}=0.
\end{displaymath}](img737.png)
![]()
bezeichnet, wenn sie der (gewichteten) Orthogonalitätsbeziehung
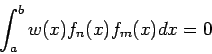
und
genügen. Der obere Index in Gl. (*) bezeichnet das Glied der Familie, der untere Index entspricht der Potenz von
. Die Normierung ist durch eine Zusatzbeziehung gegeben
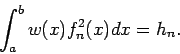
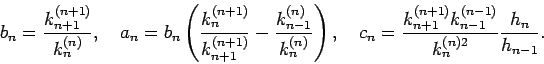
![\begin{displaymath}
f_{n}=\frac{1}{e_{n}}\frac{1}{w(x)}\frac{d^{n}}{dx^{n}}\left\{ w(x)\left[
g(x)\right] ^{n}\right\}
\end{displaymath}](img760.png)
unabhängig von
ist (das gewährleistet die Orthogonalität, Gl.(*)), und genügt einer Differenzialgleichung
und
nicht von
abhängen. Die Hermite-Polynome sind eine Familie mit
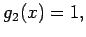
und
, die Gewichtung
, und
. Für solche Polynome gilt
und
Alle Eigenschaften der Orthogonalpolynome finden ihre Entsprechung in Eigenschaften der Erzeugungs- und Vernichtungsoperatoren.
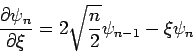
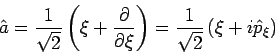
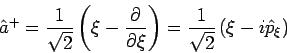
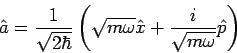
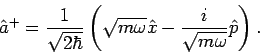
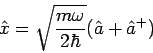
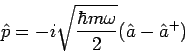
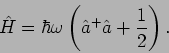
![]() -ten Zustandes kan man durch wiederhohlte
Anwendung des Operators
-ten Zustandes kan man durch wiederhohlte
Anwendung des Operators ![]() auf
auf
![]() bestimmen:
bestimmen: