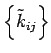 . Durch Rotation des Koordinatensystems (damit die
. Durch Rotation des Koordinatensystems (damit die 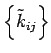 zusammenfallen)
kann man das auf die einfache Form
zusammenfallen)
kann man das auf die einfache Form
Bis jetzt haben wir nur eindimensionale Probleme betrachtet. Betrachten wir
nun als einfaches Beispiel einen 3-dimensionalen harmonischen Oszillator, mit
allgemeinem Potential
![]() ,
mit einer nicht-negativ definierten Matrix
,
mit einer nicht-negativ definierten Matrix
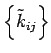 . Durch Rotation des Koordinatensystems (damit die
. Durch Rotation des Koordinatensystems (damit die ![]() ,
, ![]() und
und ![]() mit der
Hauptachsen der Matrix
mit der
Hauptachsen der Matrix
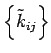 zusammenfallen)
kann man das auf die einfache Form
zusammenfallen)
kann man das auf die einfache Form
![]() bringen. Der Hamilton-Operator lautet:
bringen. Der Hamilton-Operator lautet:
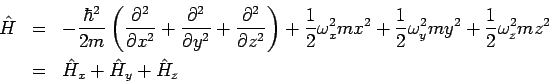
In solchem Fall (und nicht nur in solchem Fall) lohnt es sich nach der Lösung der Schrödinger-Gl.
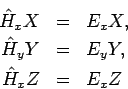
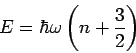
Um den Entartungsgrad zu bestimmen betrachten wir zuerst ![]() und
und ![]() . Wenn
. Wenn ![]() dann gibt es bei fixiertem
dann gibt es bei fixiertem ![]() genau
genau ![]() Möglichkeiten
Möglichkeiten ![]() auszuwählen,
auszuwählen, ![]() ist damit fixiert. Wenn jetzt
ist damit fixiert. Wenn jetzt ![]() fixiert ist, so nimmt
fixiert ist, so nimmt ![]() alle werte von 0 bis
alle werte von 0 bis ![]() an, dabei ist
an, dabei ist ![]() vorgegeben. Insgesamt haben wir dann
vorgegeben. Insgesamt haben wir dann
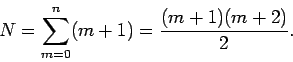
Bemerkung: Oft trifft man die Situation an, wenn das Potential als
Funktion von einigen Koordinaten verschwindet (z.B. freie Bewegung in ![]() -Richtung (Teilchen, die zu einer Linie durch einen harmonischen Potential
gebunden ist, oder die freie Bewegung in
-Richtung (Teilchen, die zu einer Linie durch einen harmonischen Potential
gebunden ist, oder die freie Bewegung in ![]() - und
- und ![]() -Richtungen (Teilchen
an einer Fläche harmonisch angebunden). In diesem Fall ist der gültige Ansatz
-Richtungen (Teilchen
an einer Fläche harmonisch angebunden). In diesem Fall ist der gültige Ansatz