Next: Klassischer Limes der Quantenmechanik.
Up: Harmonischer Oszillator
Previous: Multidimensionaler harmonischer Oszillator
Contents
Zeitunabhängiges homogenes Magnetfeld parallel zu 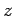 -Achse:
-Achse:
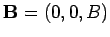 . Das klassische Teilchen im Magnetfeld
. Das klassische Teilchen im Magnetfeld 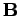 vollführt
eine Rotationsbewegung in der zu
vollführt
eine Rotationsbewegung in der zu 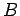 normalen Fläche, mit der Frequenz
normalen Fläche, mit der Frequenz
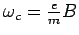 (Zyklotronfrequenz). Die Bewegung in
(Zyklotronfrequenz). Die Bewegung in 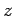 -Richtung
ist frei. Die periodische Kreisbewegung in
-Richtung
ist frei. Die periodische Kreisbewegung in 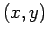 -Fläche soll
quantisiert werden. Für diese Bewegung entstehen die Energieniveaus
-Fläche soll
quantisiert werden. Für diese Bewegung entstehen die Energieniveaus
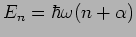 , so dass insgesamt
, so dass insgesamt
Für das Teilchen, das nur die Bewegung in 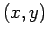 -Fläche
vorführt (2-dimensionales System, z.B. Elektronen in einem dünnen
Schicht) ist das Spektrum diskret. Wir geben hier die quantenmechanische
Betrachtung (LANDAU,1930). Das Problem ist sehr reichhaltig; wir
betrachten es hier nur als Anwendungsbeispiel zur Variablenseparation und
zur Benutzung unsere Resultaten für den harmonische Oszillator.
-Fläche
vorführt (2-dimensionales System, z.B. Elektronen in einem dünnen
Schicht) ist das Spektrum diskret. Wir geben hier die quantenmechanische
Betrachtung (LANDAU,1930). Das Problem ist sehr reichhaltig; wir
betrachten es hier nur als Anwendungsbeispiel zur Variablenseparation und
zur Benutzung unsere Resultaten für den harmonische Oszillator.
Der Hamilton-Operator für ein Teilchen im Magnetfeld:
Eichinvarianz: Für
gilt
???
Bequem: Coulomb-Eichung mit
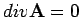 . Spezialfall: Landau-Eichung
mit
. Spezialfall: Landau-Eichung
mit
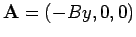 :
:
Die Lösung der Schrödinger-Gleichung
ist in Form
zu suchen. Einsetzen in die Gleichung, kleine Umgruppierung:
mit
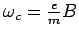 und
und
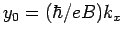 . Die Gleichung
für
. Die Gleichung
für 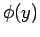
entspricht der Schrödinger-Gl. für den harmonischen Oszillator. Die
Enenrgie ist von 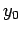 (und somit von
(und somit von 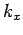 ) unabhängig. Insgesamt
gilt
) unabhängig. Insgesamt
gilt




Next: Klassischer Limes der Quantenmechanik.
Up: Harmonischer Oszillator
Previous: Multidimensionaler harmonischer Oszillator
Contents
Prof. Igor Sokolov
2005-02-14
![]() -Achse:
-Achse:
![]() . Das klassische Teilchen im Magnetfeld
. Das klassische Teilchen im Magnetfeld ![]() vollführt
eine Rotationsbewegung in der zu
vollführt
eine Rotationsbewegung in der zu ![]() normalen Fläche, mit der Frequenz
normalen Fläche, mit der Frequenz
![]() (Zyklotronfrequenz). Die Bewegung in
(Zyklotronfrequenz). Die Bewegung in ![]() -Richtung
ist frei. Die periodische Kreisbewegung in
-Richtung
ist frei. Die periodische Kreisbewegung in ![]() -Fläche soll
quantisiert werden. Für diese Bewegung entstehen die Energieniveaus
-Fläche soll
quantisiert werden. Für diese Bewegung entstehen die Energieniveaus
![]() , so dass insgesamt
, so dass insgesamt
![]() . Spezialfall: Landau-Eichung
mit
. Spezialfall: Landau-Eichung
mit
![]() :
:
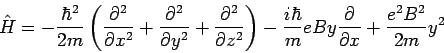
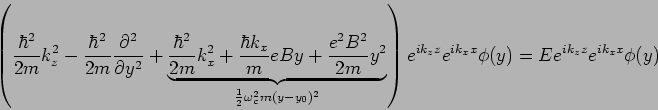
![\begin{displaymath}
\left[ -\frac{\hbar ^{2}}{2m}\frac{\partial ^{2}}{\partial y...
...}}{2m}%
k_{z}^{2}\right) }_{E-p_{z}^{2}/2m}\right] \phi (y)=0
\end{displaymath}](img844.png)