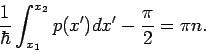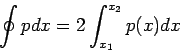Next: Quasiklassische Näherung leichgemacht
Up: Quasiklassische Näherung (WKB-Näherung)
Previous: Quasiklassische Näherung (WKB-Näherung)
Contents
Problem: Nahe an Umkehrpunkt sind die Lösungen nicht zu
verwenden, sieh Skizze.
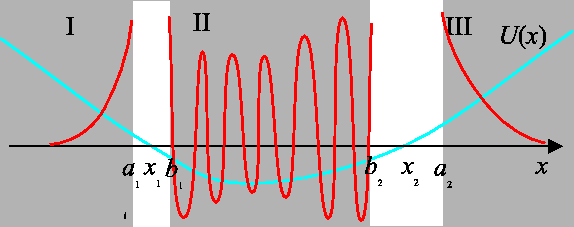
In den Gebieten in unmittelbarer Nähe der Umkehrpunkten sind diese
Näherungen unbrauchbar. Betrachten wir z.B. den Bereich 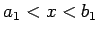 .
In diesem kleinen Bereich kann man die potentielle Energie in eine Reihe
entwickeln:
.
In diesem kleinen Bereich kann man die potentielle Energie in eine Reihe
entwickeln:
Somit erhalten wir in der Nähe des Umkehrpunkts eine Schrödinger-Gl.
Führen wir eine neue, dimensionslose Koordinate
ein, so dass
Die (nicht normierten) Ls'gen dieser Differenzialgleichung sind die AIRY-Funktionen. Wir suchen eine Lsg, die für  oszilliert und
für
oszilliert und
für 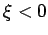 monoton abfällt. Diese Lsg. ist durch eine
Spezialfunktion
monoton abfällt. Diese Lsg. ist durch eine
Spezialfunktion
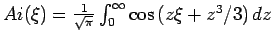 gegeben.
gegeben.
Die Grenzen des Bereichs Eq.(21) entsprechen den Werten
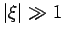 . Das asymptotische Verhalten der Lsg. ist dann gegeben
durch
. Das asymptotische Verhalten der Lsg. ist dann gegeben
durch
Kommen wir zu den Ausgangskoordinaten zurück, so erhalten wir für 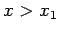
und
![$\xi ^{-1/4}=\left[ \frac{2mF}{\hbar ^{2}}(x-x_{1})\right] ^{-1/2}=1/%
\sqrt{p(x)}.$](img923.png)
Für 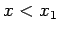 bekommt man
bekommt man
Somit kann man die Lösung and der Grenze 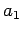 bzw.
bzw. 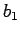 folgendermaßen schreiben:
folgendermaßen schreiben:
An der Grenze 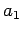 bzw.
bzw. 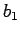 ist die Lsg.
ist die Lsg. 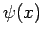 mit der
Teillösung
mit der
Teillösung 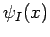 bzw.
bzw. 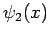 gleichzusetzen. Damit
erhält man für die Koeffizienten
gleichzusetzen. Damit
erhält man für die Koeffizienten 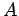 und
und 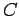 und für die Phase
und für die Phase 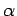
Die gleich Prozedur muß auf der Grenzen 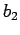 und
und 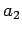 wiederholt
werden (Bemerke: Spiegelverkehrte Situation!):
wiederholt
werden (Bemerke: Spiegelverkehrte Situation!):
Die Lsg.
kann folgendermaßen umgeschrieben werden:
Diese Funktion muss in 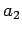 der Funktion
der Funktion 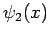 gleich sein, so
dass
gleich sein, so
dass 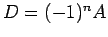 und
und
Nur dann ist der stetige Übergang in beiden Grenzbereichen
gewährleistet. Wenn wir jetzt das Phasenintegral
entlang des Weges von 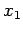 nach
nach 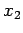 einführen, so erhalten wir
einführen, so erhalten wir
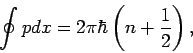 |
(23) |
die Bohr-Sommerfeldsche Quantisierungsvorschrift.




Next: Quasiklassische Näherung leichgemacht
Up: Quasiklassische Näherung (WKB-Näherung)
Previous: Quasiklassische Näherung (WKB-Näherung)
Contents
Prof. Igor Sokolov
2005-02-14

![\begin{eqnarray*}
\psi _{I}(x) &\simeq &\frac{C}{\sqrt{\left\vert p\right\vert }...
...}\sqrt{2m(U(x^{\prime })-E)}dx^{\prime
}\right] ,\qquad x>a_{2}.
\end{eqnarray*}](img910.png)
![]() .
In diesem kleinen Bereich kann man die potentielle Energie in eine Reihe
entwickeln:
.
In diesem kleinen Bereich kann man die potentielle Energie in eine Reihe
entwickeln:
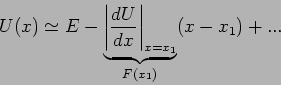
![\begin{displaymath}
\left[ \frac{\hbar ^{2}}{2m}\frac{d^{2}}{dx^{2}}+F(x-x_{1})\right] \psi
(x-x_{1})=0.
\end{displaymath}](img913.png)
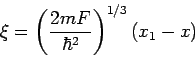
![]() . Das asymptotische Verhalten der Lsg. ist dann gegeben
durch
. Das asymptotische Verhalten der Lsg. ist dann gegeben
durch
![\begin{displaymath}
\psi (\xi )\simeq \left\{
\begin{array}{ll}
\frac{1}{2}\xi ...
...right] & \mathrm{f\ddot{u}r}\;\xi \ll -1
\end{array}\right. .
\end{displaymath}](img920.png)
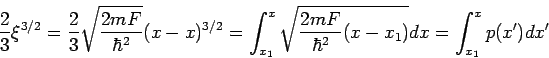
![$\xi ^{-1/4}=\left[ \frac{2mF}{\hbar ^{2}}(x-x_{1})\right] ^{-1/2}=1/%
\sqrt{p(x)}.$](img923.png)
![]() bekommt man
bekommt man
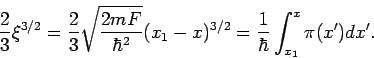
![\begin{displaymath}
\psi _{1}(x)\simeq \left\{
\begin{array}{ll}
\frac{B}{2\sqr...
...{4}\right] & \mathrm{f\ddot{u}r}\;x=b_{1}
\end{array}\right. .
\end{displaymath}](img928.png)
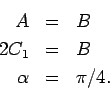
![\begin{displaymath}
\psi _{2}(x)\simeq \left\{
\begin{array}{ll}
\frac{D}{2\sqr...
...{4}\right] & \mathrm{f\ddot{u}r}\;x=b_{2}
\end{array}\right. .
\end{displaymath}](img935.png)
![\begin{displaymath}
\psi _{II}(x)=\frac{A}{\sqrt{p}}\sin \left[ \frac{1}{\hbar }...
...t_{x_{1}}^{x}p(x^{\prime })dx^{\prime }+\frac{\pi }{4}\right]
\end{displaymath}](img936.png)
![\begin{displaymath}
\psi _{II}(x)=\frac{-A}{\sqrt{p}}\sin \left[ \frac{1}{\hbar ...
...{\hbar }\int_{x_{2}}^{x_{1}}p(x^{\prime })dx^{\prime }\right]
\end{displaymath}](img937.png)