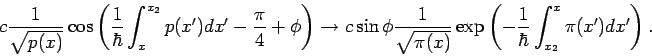Quasiklassische Näherung leichgemacht

Die Lösung in der Nähe der klassischen Umkehrpunkte müssen nur einmal gefunden werden. Dann kan mann die Konsistenzbedingungen zwischen den Lösungen vom exponentiellen und oszillerenden Typ ein für alle mal formulieren. Die allgemeine Lösung der SGl. in diesen Bereichen ist eine lineare Kombination aus 2 unabhängigen Lösungen $\psi (x)=c_{1}y_{1}(x)+c_{2}y_{2}(x)$. Die Formen von $y_{1}(x)$ und $y_{2}(x)$ in klassisch verbotenen und in klassisch erlaubten Bereichen sind bekannt. Die Konsistenzbedingungen beim Übergang zwischen den Bereichen lassen sich (anhand von der Airy-Lsg.) folgendermassen formulieren:

• wenn wir aus dem Bereich exponentieller WF (klassisch verbotener Bereich) $x<x_{1}$ zum Oszillationsbereich $x>x_{1}$ übergehen,

$$\begin{eqnarray*} \frac{c_{1}}{2}\frac{1}{\sqrt{\pi (x)}}\exp \left( -\frac{1}{\... ...int_{x_{1}}^{x}p(x^{\prime })dx^{\prime }-\frac{\pi }{4}\right) \end{eqnarray*}$$

mit $\pi (x)=\sqrt{2m(U(x)-E)}$ und $p(x)=\sqrt{2m(E-U(x))}$.

• Beim Verlassen des Bereiches gelten die gleiche Regeln, man muss nur $% x$ und $x_{1}$ austauschen. Die Richtung der Pfeile bleibt erhalten.

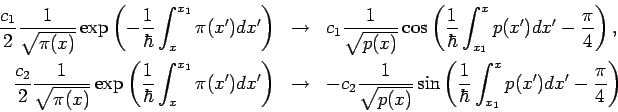
Oft ist es vernünftig statt einer komplexen Form oder statt $c_{1}\sin (...)+c_{2}\cos (...)$ die Notation $c\cos (...+\phi )$ zu benutzen. In diesem Fall

$$c\frac{1}{\sqrt{p(x)}}\cos \left( \frac{1}{\hbar }\int_{x}^{... ...{\hbar }\int_{x_{2}}^{x}\pi (x^{\prime })dx^{\prime }\right) .$$