



Next: Beispiel: Potentialtopf. Diskretes Spektrum
Up: Klassischer Limes der Quantenmechanik.
Previous: Klassischer Limes der Quantenmechanik.
Contents
Die quasiklassische (WKB: für Wentzel-Kramers-Brillouin) Näherung
ist ein Verfahren zur Lösung der Gl.
woraus die WF des stationären Zustandes als
folgt. Die Lösung wird als formale Entwicklung nach Potenzen von 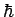 gesucht:
gesucht:
Ist die Voraussetzung
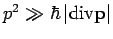 erfüllt, sind die höheren Glieder der Reihe bedeutend kleiner als
die vorhergehenden. Die Lösung kann durch Iteration bestimmt werden:
erfüllt, sind die höheren Glieder der Reihe bedeutend kleiner als
die vorhergehenden. Die Lösung kann durch Iteration bestimmt werden:
- 0. Ordnung
- 1. Ordnung
- 2. Ordnung
usw.
Gewöhnlich beschränkt man sich auf 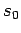 und
und 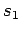 .
.
Beispiel: Eindimensionale Bewegung.
usw, mit
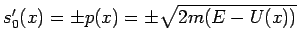 (die Funktion
(die Funktion 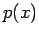 fällt mit dem Betrag des klassischen Impulses zusammen falls
fällt mit dem Betrag des klassischen Impulses zusammen falls 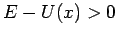 ist). Damit
ist). Damit
Aus der 2. Gleichung folgt dann
(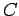 -Integrationskonstante). Daher ist die allgemeine Lösung
-Integrationskonstante). Daher ist die allgemeine Lösung
Der Bereich 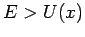 wird als klassisch erlaubter Bereich
bezeichnet. In diesem Bereich kann man die WF als Funktion schreiben, die
von 2 Parameter abhängig ist
wird als klassisch erlaubter Bereich
bezeichnet. In diesem Bereich kann man die WF als Funktion schreiben, die
von 2 Parameter abhängig ist
![\begin{displaymath}
\psi (x)=\frac{A}{\sqrt{p}}\sin \left[ \frac{1}{\hbar }\int_{a}^{x}p(x^{%
\prime })dx^{\prime }+\alpha \right] .
\end{displaymath}](img897.png) |
(20) |
Die Amplitude der WF ist proportional zu 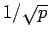 . Die
Aufenthaltwahrscheinlichkeit in kleinen Volumen ist im Wesentlichen
proportional zu
. Die
Aufenthaltwahrscheinlichkeit in kleinen Volumen ist im Wesentlichen
proportional zu
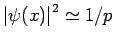 , d.h. umgekehrt
proportional zu der Geschwindigkeit des klassischen Teilchens.
, d.h. umgekehrt
proportional zu der Geschwindigkeit des klassischen Teilchens.
Die Werte 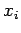 , für die
, für die 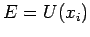 , entsprechen der Umkehrpunkten. Das sind die Ruhepunkte des klassischen Teilchen. In diesen
Punkten wird die quasiklassische Näherung unbrauchbar. Nahe an diesen
Punkten
, entsprechen der Umkehrpunkten. Das sind die Ruhepunkte des klassischen Teilchen. In diesen
Punkten wird die quasiklassische Näherung unbrauchbar. Nahe an diesen
Punkten
Aus der Bedingung
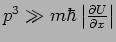 folgt, dass der Gültigkeitsbereich der quasiklassischen
Näherung den Abständen
folgt, dass der Gültigkeitsbereich der quasiklassischen
Näherung den Abständen
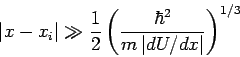 |
(21) |
entspricht.
Der Bereich 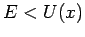 wird als klassisch nicht erlaubter Bereich
bezeichnet. In diesem Bereich ist
wird als klassisch nicht erlaubter Bereich
bezeichnet. In diesem Bereich ist 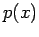 imaginär:
imaginär:
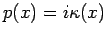 .
Damit ist die Lösung
.
Damit ist die Lösung
![\begin{displaymath}
\psi (x)=\frac{C}{\sqrt{\left\vert p\right\vert }}\exp \left...
...{\hbar }\int_{a}^{x}\kappa (x^{\prime
})dx^{\prime }\right] .
\end{displaymath}](img908.png) |
(22) |
Die quasiklassische Funktionen (20) und (22) sollen
im Umkehrpunkt aneinander angeschlossen werden (vgl. rechteckige
Potentialtopf).
Subsections




Next: Beispiel: Potentialtopf. Diskretes Spektrum
Up: Klassischer Limes der Quantenmechanik.
Previous: Klassischer Limes der Quantenmechanik.
Contents
Prof. Igor Sokolov
2005-02-14
![\begin{displaymath}
\psi (\mathbf{r})=\exp \left[ \frac{i}{\hbar }s(\mathbf{r})\right]
\end{displaymath}](img879.png)
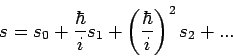
![]() und
und ![]() .
.
![\begin{eqnarray*}
\left[ s_{0}^{\prime }(x)\right] &=&p^{2}(x) \\
2s_{1}^{\prim...
...\left(
s_{1}^{\prime }(x)\right) ^{2}\right] /s_{0}^{\prime }(x)
\end{eqnarray*}](img888.png)
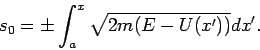
![\begin{displaymath}
\psi (x)=\frac{C}{\sqrt{\left\vert p(x)\right\vert }}\exp \l...
...rac{i}{\hbar }\int_{a}^{x}p(x^{\prime
})dx^{\prime }\right] .
\end{displaymath}](img895.png)
![]() , für die
, für die ![]() , entsprechen der Umkehrpunkten. Das sind die Ruhepunkte des klassischen Teilchen. In diesen
Punkten wird die quasiklassische Näherung unbrauchbar. Nahe an diesen
Punkten
, entsprechen der Umkehrpunkten. Das sind die Ruhepunkte des klassischen Teilchen. In diesen
Punkten wird die quasiklassische Näherung unbrauchbar. Nahe an diesen
Punkten
![\begin{displaymath}
p^{2}=2m\left[ E-U(x)\right] \simeq 2m\left\vert \frac{dU}{dx}\right\vert \left\vert
x-x_{i}\right\vert .
\end{displaymath}](img902.png)
![]() wird als klassisch nicht erlaubter Bereich
bezeichnet. In diesem Bereich ist
wird als klassisch nicht erlaubter Bereich
bezeichnet. In diesem Bereich ist ![]() imaginär:
imaginär:
![]() .
Damit ist die Lösung
.
Damit ist die Lösung