



Next: Operatoren für physikalische Größen
Up: Quasiklassische Näherung (WKB-Näherung)
Previous: Quasiklassische Näherung leichgemacht
Contents
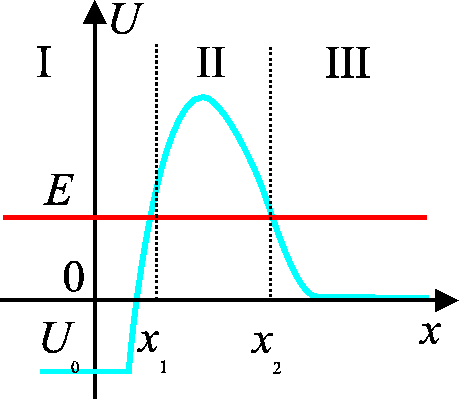
Betrachten wir die quasiklassische Näherung für die Zustände
aus kontinuierlichem Spektrum. Die einfallende Welle kommt aus dem Bereich
I, wobei das Potential verschwindet
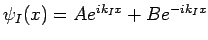 . Im Gebiet III gibt es auslaufende Teilchen. Weit von dem Wall verschwindet
das Potential, so ist die WF
. Im Gebiet III gibt es auslaufende Teilchen. Weit von dem Wall verschwindet
das Potential, so ist die WF
Wir interessieren uns für das Durchdringen des Walls und definieren den
Durchlaßkoeffizienten 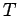 :
:
Bemerkung: Der Wahrscheinlichkeitsstrom in der einfallede Welle ist
In dem Gebiet III hat man
(richtige Dimension:
Aus der Stromerhaltung folgt
Zunächst betrachten wir den Fall
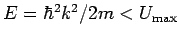 . Zur
Berechnung dieser Größen muß man die Bewegung des Teilchens im
Bereich II untersuchen.
. Zur
Berechnung dieser Größen muß man die Bewegung des Teilchens im
Bereich II untersuchen.
Es ist einfacher, vom Bereich III anzufangen (nur 1 Welle), 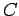 festsetzen
und
festsetzen
und 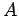 und
und 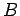 als Funktionen von
als Funktionen von 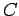 zu bestimmen. Setzen wir
einfachheitshalber
zu bestimmen. Setzen wir
einfachheitshalber
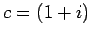 (d.h.
(d.h.
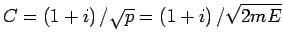 ). Die Lsg. in diesem Bereich ist dann:
). Die Lsg. in diesem Bereich ist dann:
oder
Im Bereich II wird diese Lösung zu einer rein exponentiell abfallenden Lösung
mit
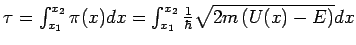 .
.
Im Bereich I benutzen wir eine Lösung
(mit i.A. komplexen Koeffizient 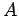 ). Die Konsistenzbedingungen im Punkt
). Die Konsistenzbedingungen im Punkt 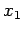 ergeben dann:
ergeben dann:
so dass
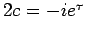 . Da
. Da
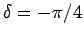 reell ist, ergeben sich die
praktisch gleichen Amplituden für einlaufende und der reflektierte Welle,
da
reell ist, ergeben sich die
praktisch gleichen Amplituden für einlaufende und der reflektierte Welle,
da
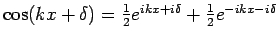 . Daher
. Daher
mit
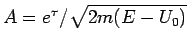 . Der Durchlasskoeffizient ist dann:
. Der Durchlasskoeffizient ist dann:
Für die Anwendbarkeit der WKB-Methode ist es wichtig, dass der Wall eine
Breite von ''mehreren Wellenlängen'' hat, d.h. 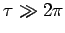 . Damit
ist der Durchlasskoeffizient
. Damit
ist der Durchlasskoeffizient 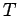 sehr klein,
sehr klein,
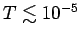 . Das erklärt auch die praktische Gleichheit der Amplituden der einlaufenden und
der reflektierten Welle. Der typische Wert des Durchlasskoeffizienten
. Das erklärt auch die praktische Gleichheit der Amplituden der einlaufenden und
der reflektierten Welle. Der typische Wert des Durchlasskoeffizienten
gilt für den allgemeinen Fall. Der Reflexionskoeffizient, den wir in unserer
einfachen Betrachtung gleich 1 gesetzt haben, kann nachträglich als
bestimmt werden.
Anwendungsbeispiele: kalte Elektronenemission aus einem Metall,
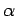 -Zerfall, u.s.w.
-Zerfall, u.s.w.




Next: Operatoren für physikalische Größen
Up: Quasiklassische Näherung (WKB-Näherung)
Previous: Quasiklassische Näherung leichgemacht
Contents
Prof. Igor Sokolov
2005-02-14
![]() . Im Gebiet III gibt es auslaufende Teilchen. Weit von dem Wall verschwindet
das Potential, so ist die WF
. Im Gebiet III gibt es auslaufende Teilchen. Weit von dem Wall verschwindet
das Potential, so ist die WF
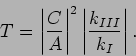
![\begin{eqnarray*}
J_{I} &=&\mbox{Re}\left[ \Psi _{I}^{*}\frac{\hbar }{im}\nabla ...
... _{I}\right] =%
\frac{\hbar k_{I}}{m}\left( A^{2}-B^{2}\right) .
\end{eqnarray*}](img956.png)
![\begin{displaymath}
\left[ J\right] =\left[ \frac{ML^{2}}{T}\frac{1}{L}\frac{1}{M}\right]
=\left[ v\right]
\end{displaymath}](img958.png)
![]() . Zur
Berechnung dieser Größen muß man die Bewegung des Teilchens im
Bereich II untersuchen.
. Zur
Berechnung dieser Größen muß man die Bewegung des Teilchens im
Bereich II untersuchen.
![]() festsetzen
und
festsetzen
und ![]() und
und ![]() als Funktionen von
als Funktionen von ![]() zu bestimmen. Setzen wir
einfachheitshalber
zu bestimmen. Setzen wir
einfachheitshalber
![]() (d.h.
(d.h.
![]() ). Die Lsg. in diesem Bereich ist dann:
). Die Lsg. in diesem Bereich ist dann:
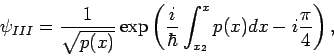
![\begin{displaymath}
\psi _{III}=\frac{1}{\sqrt{p(x)}}\left[ \cos \left( \frac{1}...
...hbar }%
\int_{x_{2}}^{x}p(x)dx-\frac{\pi }{4}\right) \right] .
\end{displaymath}](img965.png)
![\begin{eqnarray*}
\psi _{II} &=&-i\frac{1}{\sqrt{\pi (x)}}\exp \left( \frac{1}{\...
...ft( -\frac{1}{\hbar }%
\int_{x_{1}}^{x}\pi (x)dx\right) \right]
\end{eqnarray*}](img966.png)
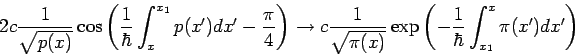
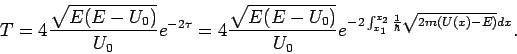
![]() -Zerfall, u.s.w.
-Zerfall, u.s.w.