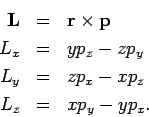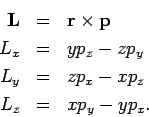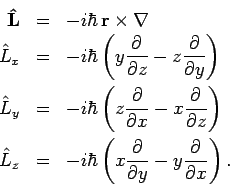Next: Eigenwerte und Eigenfunktionen des
Up: Operatoren für physikalische Größen
Previous: Die Fluktuationen. Eigenfunktionen und
Contents
Klassisch gilt
Anhand des Korrespondenzprinzips
Aus den Vertauschbarkeitsregeln
![$\left[ \hat{q}_{i},\hat{q}_{k}\right] =0$](img1057.png) ,
,
![$\left[ \hat{p}_{i},\hat{p}_{k}\right] =0$](img1058.png) ,
,
![$\left[ \hat{q}_{i},\hat{p}%
_{k}\right] =i\hbar \delta _{ik}$](img1059.png) für die Koordinaten und Impulse folgt:
für die Koordinaten und Impulse folgt:
und die weitere zyklische Umstellungen 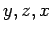 und
und 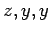 . Ferner kann man
zeigen, dass
. Ferner kann man
zeigen, dass
und
und zyklische Permutationen, sowie
und zyklische Permutationen.
Subsections
Prof. Igor Sokolov
2005-02-14