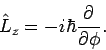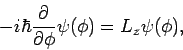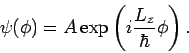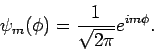Next: Bemerkung: Übergang zur Kugelkoordinaten:
Up: Beispiel: das Drehmoment
Previous: Beispiel: das Drehmoment
Contents
Übergang zu Kugelkoordinaten ergibt
Die Gleichung für die Eigenwerte
die Variable 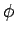 ändert sich in Grenzen
ändert sich in Grenzen
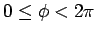 . Die Lösungen sind
. Die Lösungen sind
Damit die Funktionen 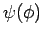 eindeutig sind, muß die periodische
Randbedingung
eindeutig sind, muß die periodische
Randbedingung
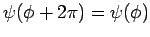 erfüllt werden. Daher
ist
erfüllt werden. Daher
ist 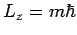 , mit
, mit
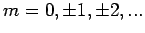 . Die normierten WF haben die
Gestalt
. Die normierten WF haben die
Gestalt
Subsections
Prof. Igor Sokolov
2005-02-14