



Next: Eigenwerte und Eigenfunktionen des
Up: Eigenwerte und Eigenfunktionen des
Previous: Eigenwerte und Eigenfunktionen des
Contents
Zu den Transformationen
gehören die inversen Transformationen
Daher
Dann gilt:
Die zwei anderen Komponenten lauten:
und
Der Operator
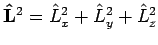 hat eine Darstellung
hat eine Darstellung
Prof. Igor Sokolov
2005-02-14
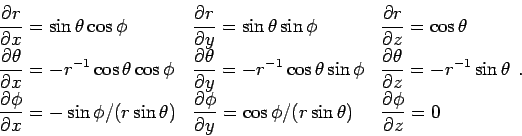
![\begin{eqnarray*}
\hat{L}_{z} &=&-i\hbar \left( x\frac{\partial }{\partial y}-y\...
...i }\right] \\
&=&....=-i\hbar \frac{\partial }{\partial \phi }.
\end{eqnarray*}](img1081.png)
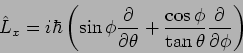
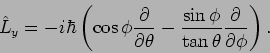
![\begin{displaymath}
\mathbf{\hat{L}}^{2}=-\hbar ^{2}\left[ \frac{1}{\sin \theta ...
...{2}\theta }\frac{\partial ^{2}}{\partial \phi ^{2}}%
\right] .
\end{displaymath}](img1085.png)