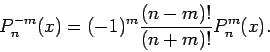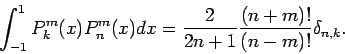Next: Schlussfolgerungen:
Up: Beispiel: das Drehmoment
Previous: Bemerkung: Übergang zur Kugelkoordinaten:
Contents
Damit
Der Definitionsbereich der WF:
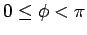 und Randbedingungen sind:
zyklisch in
und Randbedingungen sind:
zyklisch in 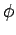 :
:
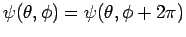 (Eindeutigkeit), natürlich in
(Eindeutigkeit), natürlich in 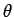 .
.
Variablentrennung:
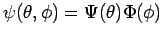 .
.
oder
Man kann
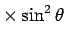 mutiplizieren. Die Gl. zerfällt dann
in nur von
mutiplizieren. Die Gl. zerfällt dann
in nur von 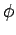 und nur von
und nur von 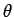 abhängige Teile. Lsg. für
abhängige Teile. Lsg. für
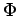 entspricht dem vorherigen:
entspricht dem vorherigen: 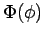 sind die Eigenfunktionen
von
sind die Eigenfunktionen
von 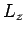 :
:
mit 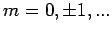 - Azimuthalquantenzahl (oder magnetische Quantenzahl).
Die Gl. für
- Azimuthalquantenzahl (oder magnetische Quantenzahl).
Die Gl. für 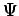
Das ist die assoziierte LEGENDREsche Gl.
Bemerkung: nimmt man 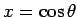 so erhält man nach einer
einfachen Transformation
so erhält man nach einer
einfachen Transformation
![\begin{displaymath}
(1-x^{2})\frac{d^{2}}{dx^{2}}\Psi (x)-2x\frac{d}{dx}\Psi (x)...
...frac{L^{2}}{\hbar^2 }-\frac{m^{2}}{1-x^{2}}\right] \Psi (x)=0,
\end{displaymath}](img1101.png) |
(27) |
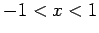 . Die integrablen Ls'gen existieren nur für
. Die integrablen Ls'gen existieren nur für
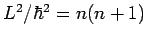 ,
das sind die assoziierten Legendre-Polynome
,
das sind die assoziierten Legendre-Polynome 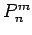 . Für
. Für 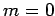 bekommen wir die eigentliche Legendre-Gl.
bekommen wir die eigentliche Legendre-Gl.
Die Situation ist ''wie immer'': wenn man die Lsg. als allgemeine
Potenzreihe hinschreibt, kann man die Koeffizienten anhand von
Rekurrenzbedingungen bestimmen, siehe z.B.
G.B. Arfken, H.J. Weber, Mathematical methods for Physicists, Harcourt, San
Diego, 2001). Die Analyse der Konvergenz der Reihe zeigt, dass wenn diese nicht
abbricht, so konvergiert die Reihe für alle 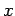 ,
, 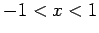 , divergiert aber
für
, divergiert aber
für
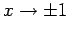 und hat solch starke Divergenz, dass die Funktionen
nicht mehr integrabel sind.
Bricht die Reihe ab (für
und hat solch starke Divergenz, dass die Funktionen
nicht mehr integrabel sind.
Bricht die Reihe ab (für
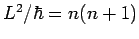 ), so ist diese ein Polynom in
), so ist diese ein Polynom in 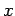 .
In diesem Fall divergiert Sie nicht, und es gilt
.
In diesem Fall divergiert Sie nicht, und es gilt 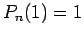 ,
,
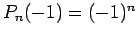 .
.
Die Legendre-Polynome bekommt man als
Die Legendre-Polynome erfüllen mehrere Rekurrenzbedingungen (siehe
G.B. Arfken, H.J. Weber), deren Existenz weist auf die Möglichkeit der Einführung der
Stufenoperatoren (analog zu Erzeugungs- und Vernichtungsoperatoren)
hin. Die können aber auch auf einem physikalischen Wege eingeführt
werden (später!). Man kann zeigen, dass die Ls'gen 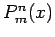 für
für 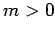 aus den Ls'gen mit
aus den Ls'gen mit 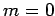 durch
durch
bestimmt werden können (um das zu zeigen schreibe man die Gl. für 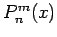 anhand der Gl. für
anhand der Gl. für 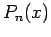 hin und überzeuge sich, das diese Gl. mit der
Gl.(27) identisch ist). Die nichtverschwindenden Ls'gen gibt es nur für
hin und überzeuge sich, das diese Gl. mit der
Gl.(27) identisch ist). Die nichtverschwindenden Ls'gen gibt es nur für
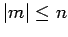 . Die Ls'gen mit negativem
. Die Ls'gen mit negativem 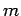 könen anhand der Ls'gen mit positiven
könen anhand der Ls'gen mit positiven
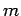 bestimmt werden
bestimmt werden
Orthogonalität: Es gilt:
Subsections




Next: Schlussfolgerungen:
Up: Beispiel: das Drehmoment
Previous: Bemerkung: Übergang zur Kugelkoordinaten:
Contents
Prof. Igor Sokolov
2005-02-14
![\begin{displaymath}
\left[ \frac{1}{\sin \theta }\frac{\partial }{\partial \thet...
...phi ^{2}}+\frac{L^{2}}{\hbar^2}\right] \psi
(\theta ,\phi )=0.
\end{displaymath}](img1088.png)
![]() .
.
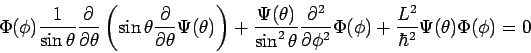
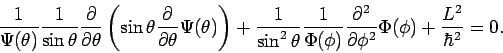
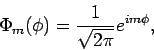
![\begin{displaymath}
\frac{1}{\sin \theta }\frac{d}{d\theta }\left( \sin \theta \...
...ar^2 }-\frac{m^{2}}{\sin
^{2}\theta }\right] \Psi (\theta )=0.
\end{displaymath}](img1099.png)
![]() so erhält man nach einer
einfachen Transformation
so erhält man nach einer
einfachen Transformation