



Next: Die räumliche Struktur der
Up: Bewegung in einem Coulomb-Feld.
Previous: Bewegung in einem Coulomb-Feld.
Contents
- Zusammenhang mit Lauerre-Polynomen (wohlbekannten Speziallfall mit
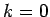 )
)
- Koeffizienten:
so dass
- Erzeugende Funktion:
- Rodrieges Formula
- Rekurrenzbeziehungen:
- Gewichtung und Normierung:
Da die Winkelanteile
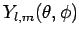 der Wellenfunktionen ein
orthonormiertes System der Funktionen bilden,
der Wellenfunktionen ein
orthonormiertes System der Funktionen bilden,
sind die Mittelwerte von 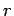 nur durch die radiale Wellenfunktion bestimmt:
nur durch die radiale Wellenfunktion bestimmt:
Für die Potenzen
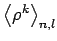 gilt eine nützliche KRAMERS-Relation:
gilt eine nützliche KRAMERS-Relation:
für 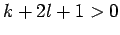 (siehe z.B. Nolting, Vol 5/2, §6.2 und Aufgabe 6.2.5).
Dann genügt es
(siehe z.B. Nolting, Vol 5/2, §6.2 und Aufgabe 6.2.5).
Dann genügt es
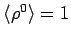 und
und
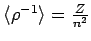 separat auszurechnen,
um die anderen Momenten von
separat auszurechnen,
um die anderen Momenten von 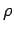 zu bestimmen.
zu bestimmen.




Next: Die räumliche Struktur der
Up: Bewegung in einem Coulomb-Feld.
Previous: Bewegung in einem Coulomb-Feld.
Contents
Prof. Igor Sokolov
2005-02-14
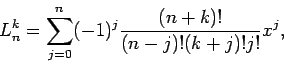
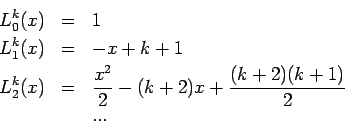
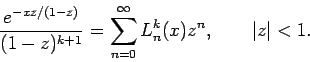
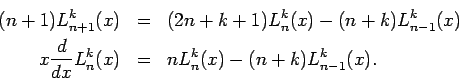
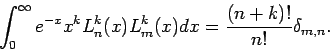
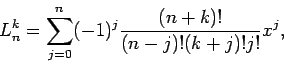
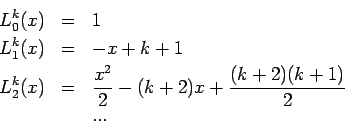
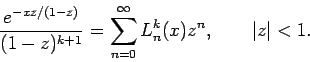
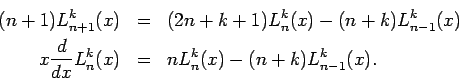
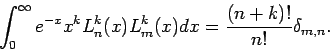
![]() der Wellenfunktionen ein
orthonormiertes System der Funktionen bilden,
der Wellenfunktionen ein
orthonormiertes System der Funktionen bilden,
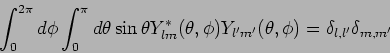
![\begin{displaymath}
\left\langle \rho ^{k}\right\rangle _{n,l}=\int_{0}^{\infty }d\rho ~\rho
^{2+k}\left[ F(\rho )\right] ^{2}.
\end{displaymath}](img1215.png)
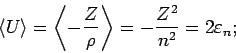
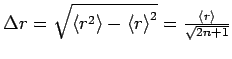 . Für
. Für