



Next: Das maximalen Satz der
Up: Statistik der Messwerten im
Previous: Ideale Messungen
Contents
Nicht alle Messgrößen können gleichzeitig gemessen werden (z.B.
Impuls und Koordinate, lt. der Unschärferelation). Diejenige Messbaren,
die gleichzeitig scharfe Werte besitzen werden als verträglich
bezeichnet. Wie wir schon am Beispielen gesehen haben, entsprechen solche
Messbaren den kommutierenden Operatoren.
Betrachten wir 2 Observablen, 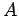 und
und 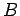 . Nehmen wir an, dass die
Operatoren
. Nehmen wir an, dass die
Operatoren  und
und 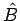 die gleiche Eigenfunktion
die gleiche Eigenfunktion 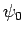 haben, d.h.
haben, d.h.
und
Wenn ein physikalisches System zur Zeit der Messung in dem Zustand
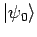 sich befindet, so wird die Messung von
sich befindet, so wird die Messung von 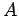 und
und 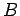 die Werte
die Werte 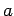 und
und 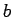 liefern. Eine notwendige Bedingung dafür ist
liefern. Eine notwendige Bedingung dafür ist
Diese Gleichung ist automatisch erfüllt, wenn
i.e. wenn die Operatoren  und
und 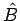 kommutieren.
kommutieren.
- Wenn 2 Operatoren
 und
und 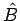 kommutieren, so haben sie
das gleiche VONS von Eigenfunktionen, und umgekehrt, wenn 2 Operatoren das
gleiche VONS von Eigenfunktionen besitzen, so kommutieren sie.
kommutieren, so haben sie
das gleiche VONS von Eigenfunktionen, und umgekehrt, wenn 2 Operatoren das
gleiche VONS von Eigenfunktionen besitzen, so kommutieren sie.
- Die Messbaren, die den kommutierenden Operatoren
 und
und 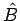 entsprechen, sind verträglich, d.h. das Resultat der
Messungen hängt nicht davon ab, welcher Wert,
entsprechen, sind verträglich, d.h. das Resultat der
Messungen hängt nicht davon ab, welcher Wert, 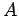 und
und 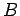 , zuerst
gemessen wird. Nach solcher Messung wird die WF des Systemes einer gemeinsamen
WF der Eigenwerte
, zuerst
gemessen wird. Nach solcher Messung wird die WF des Systemes einer gemeinsamen
WF der Eigenwerte 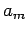 und
und 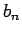 entsprechen.
entsprechen.
Beweis: Nehmen wir an, dass
![$\left[ \hat{A},\hat{B}\right] =0$](img1041.png) .
Sei
.
Sei 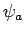 eine EF von
eine EF von  zur EW
zur EW 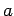 . Diese Fkt. kann über
das VONS von Operator
. Diese Fkt. kann über
das VONS von Operator 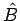 entwickelt werden:
entwickelt werden:
wobei
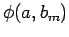 eine EF von
eine EF von 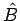 zur EW
zur EW 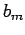 ist (nicht
unbedingt auf 1 normiert). Es kann stets so gemacht werden, dass alle EF
ist (nicht
unbedingt auf 1 normiert). Es kann stets so gemacht werden, dass alle EF
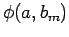 zu unterschiedlichen EW
zu unterschiedlichen EW 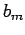 angehören (wenn
es nicht so ist, und den Wert
angehören (wenn
es nicht so ist, und den Wert 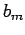 entartet ist, wählen wir einfach
die entsprechende Linearkombination von
entartet ist, wählen wir einfach
die entsprechende Linearkombination von
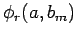 als die
EF). Führen wir eine Funktion
als die
EF). Führen wir eine Funktion
ein.
Da  und
und 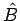 kommutieren, gilt
kommutieren, gilt
Da alle EW 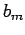 unterschiedlich sind, sind die WF linear unabhängig.
Gleichzeitig gilt aber
unterschiedlich sind, sind die WF linear unabhängig.
Gleichzeitig gilt aber
Das ist aber nur dann möglich, wenn jede
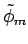 verschwindet.
verschwindet. 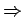
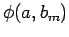 sind gleichzeitig die EF von
sind gleichzeitig die EF von
 .
.
Betrachten wir nun das VONS von EF von  ,
,
Diese Fkt'en können dann als
dargestellt werden, wobei
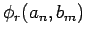 die EF sowohl von
die EF sowohl von
 als auch von
als auch von 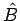 sind. Die Fkt.
sind. Die Fkt.
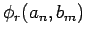 brauchen nicht zueinander orthogonal sein, können
aber dann orthogonalisiert werden. Nach Orthogonalisierung erhalten wir ein
VONS
brauchen nicht zueinander orthogonal sein, können
aber dann orthogonalisiert werden. Nach Orthogonalisierung erhalten wir ein
VONS
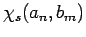 so dass
so dass
Die Funktionen 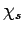 bilden das gemeinsames VONS der EF von
bilden das gemeinsames VONS der EF von  und
und 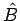 .
.
Umgekehrt, bilden 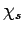 das gemeinsame VONS der EF von
das gemeinsame VONS der EF von  und
und 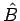 , so gilt
, so gilt
so dass
![$\left[ \hat{A},\hat{B}\right] \chi _{s}=0$](img1474.png) . Da jede WF
. Da jede WF 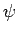 über entsprechende VONS entwickelt werden kann, so
über entsprechende VONS entwickelt werden kann, so
![$\left[ \hat{A},\hat{B}\right] \psi =0$](img1475.png) und
und
- Die hintereinender geschalteten Filter für verschiedene
verträgliche Variablen schaffen die Zustände mit mehreren
vorgegebenen Eigenschaften (die Messung der nicht-verträglichen
Variablen, z.B. die Koordinatenmessung nach dem Impulsmessung, stört die
Genauigkeit der vorherigen Vorgabe).
Bemerkung: Aus der kommutierenden Observablen 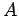 und
und 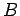 kann man neue Observable bilden,
kann man neue Observable bilden, 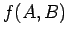 . Die Funktion der 2 Operatoren
. Die Funktion der 2 Operatoren
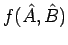 , auf
, auf 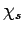 angewandt, ergibt
angewandt, ergibt
Subsections




Next: Das maximalen Satz der
Up: Statistik der Messwerten im
Previous: Ideale Messungen
Contents
Prof. Igor Sokolov
2005-02-14
![]() und
und ![]() . Nehmen wir an, dass die
Operatoren
. Nehmen wir an, dass die
Operatoren ![]() und
und ![]() die gleiche Eigenfunktion
die gleiche Eigenfunktion ![]() haben, d.h.
haben, d.h.
![$\left[ \hat{A},\hat{B}\right] =0$](img1041.png) .
Sei
.
Sei ![]() eine EF von
eine EF von ![]() zur EW
zur EW ![]() . Diese Fkt. kann über
das VONS von Operator
. Diese Fkt. kann über
das VONS von Operator ![]() entwickelt werden:
entwickelt werden:
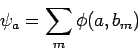
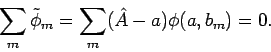
![]() ,
,
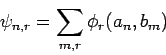
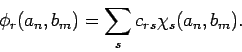
![]() das gemeinsame VONS der EF von
das gemeinsame VONS der EF von ![]() und
und ![]() , so gilt
, so gilt
![$\left[ \hat{A},\hat{B}\right] \chi _{s}=0$](img1474.png) . Da jede WF
. Da jede WF ![$\left[ \hat{A},\hat{B}\right] \psi =0$](img1475.png) und
und
![]() und
und ![]() kann man neue Observable bilden,
kann man neue Observable bilden, ![]() . Die Funktion der 2 Operatoren
. Die Funktion der 2 Operatoren
![]() , auf
, auf ![]() angewandt, ergibt
angewandt, ergibt