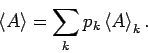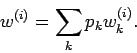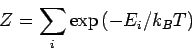Das VONS vom Operator des Messbaren ![]() werden wir als Basissystem von
werden wir als Basissystem von ![]() betrachten. Wenn alle EW von
betrachten. Wenn alle EW von ![]() nicht
entartet sind, ist dieses System eindeutig definiert (bis auf Phasen). Wenn
Entartung vorliegt, so können die entsprechenden EF unterschiedlicherweise
orthogonalisiert werden.
nicht
entartet sind, ist dieses System eindeutig definiert (bis auf Phasen). Wenn
Entartung vorliegt, so können die entsprechenden EF unterschiedlicherweise
orthogonalisiert werden.
Wenn es noch eine Messbare ![]() gibt, die mit
gibt, die mit ![]() verträglich ist, kann
es sein, dass
verträglich ist, kann
es sein, dass ![]() und
und ![]() zusammen ein eindeutiges VONS der EF
besitzen. Wenn das gemeinsame VONS von
zusammen ein eindeutiges VONS der EF
besitzen. Wenn das gemeinsame VONS von ![]() und
und ![]() trotzden
nicht eindeutig definiert ist, so gibt es eine dritte, mit dieser zweier
verträgliche Messbare
trotzden
nicht eindeutig definiert ist, so gibt es eine dritte, mit dieser zweier
verträgliche Messbare ![]() , u.s.w. Man sagt, dass die Messbaren
, u.s.w. Man sagt, dass die Messbaren ![]() ein vollständigen Satz der verträglichen Messbaren bilden,
wenn die Operatoren
ein vollständigen Satz der verträglichen Messbaren bilden,
wenn die Operatoren
![]() ein eindeutig definiertes VONS
von Eigenfunktionen besitzen. Daher existiert nur
eine WF, die dem Eigenwerten
ein eindeutig definiertes VONS
von Eigenfunktionen besitzen. Daher existiert nur
eine WF, die dem Eigenwerten ![]() angehört. Die
gleichzeitige Messung von
angehört. Die
gleichzeitige Messung von ![]() definiert dann eindeutig die
Wellenfunktion
definiert dann eindeutig die
Wellenfunktion
![]() nach der Messung.
nach der Messung.
Ein gemischter Zustand zur Zeit ![]() der Präparation wird durch die
Menge der Wellenfunktionen
der Präparation wird durch die
Menge der Wellenfunktionen
![]() (der
Index entspricht allen durch der Messung nicht aufgelösten
Quantenzahlen), mit statistischen Gewichten (Wahrscheinlichkeiten)
(der
Index entspricht allen durch der Messung nicht aufgelösten
Quantenzahlen), mit statistischen Gewichten (Wahrscheinlichkeiten)
![]() ,
,
![]() (d.h., der Zustand des Systems ist
nicht als reiner Zustand eindeutig definiert, das System befindet sich mit
gewisser Wahrscheinlichkeit in einem mit Messergebnissen verträglichen
reinen Zustand). Seien
(d.h., der Zustand des Systems ist
nicht als reiner Zustand eindeutig definiert, das System befindet sich mit
gewisser Wahrscheinlichkeit in einem mit Messergebnissen verträglichen
reinen Zustand). Seien
![]() die Ls'gen der
Schrödingergl. (oder der anderen Gl., die die dynamische Evolution der
WF beschreibt), mit Anfangsbedingungen
die Ls'gen der
Schrödingergl. (oder der anderen Gl., die die dynamische Evolution der
WF beschreibt), mit Anfangsbedingungen
![]() . Das System zur Zeit
. Das System zur Zeit ![]() wird durch
wird durch
![]() beschrieben, mit gleichen Wahrscheinlichkeiten
beschrieben, mit gleichen Wahrscheinlichkeiten
![]() . Sei
. Sei
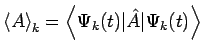 der Mittelwert der Messbaren
der Mittelwert der Messbaren ![]() zur Zeit
zur Zeit ![]() im
Zustand
im
Zustand ![]() . Dann ist der Mittelwert von
. Dann ist der Mittelwert von ![]() in einem gemischten Zustand
in einem gemischten Zustand