



Next: Zeitliche Änderung der statistischen
Up: Statistik der Messwerten im
Previous: Das maximalen Satz der
Contents
4 Grundregeln:
Durch die wiederhohlte Anwendung von (40) bekommt man
Anhand dieser Regel kann man auch den Kommutator
![$\left[ \hat{A},f(\hat{B})\right] $](img1510.png) ausrechnen, falls
ausrechnen, falls 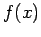 eine konvergierende Taylor-Reihe besitzt.
eine konvergierende Taylor-Reihe besitzt.
Beispiele: Kommutationseigenschaften für Drehimpuls:
Die Komponenten des Drehimpulses kommutieren nicht miteinander. Die Komponenten
des Drehimpulses besitzen keine gemeinsamen VONS. I.A. können die 2
Komponenten des Drehimpulses gleichzeitig gemessen werden (abgesehen von der
Situation für
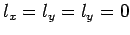 ). Aus (40) folgt
). Aus (40) folgt
Zusammenaddiert
mit
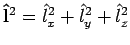 .
Die Operatoren
.
Die Operatoren
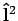 und
und 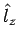 kommutieren, d.h.
sie können gleichzeitig gemessen werden. Die Paare
kommutieren, d.h.
sie können gleichzeitig gemessen werden. Die Paare
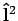 und
und 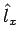 und
und
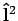 und
und 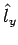 besitzen
die gleiche Eigenschaft.
besitzen
die gleiche Eigenschaft.




Next: Zeitliche Änderung der statistischen
Up: Statistik der Messwerten im
Previous: Das maximalen Satz der
Contents
Prof. Igor Sokolov
2005-02-14
![$\displaystyle \left[ \hat{A},\hat{B}\right]$](img1501.png)
![$\displaystyle -\left[ \hat{B},\hat{A}\right] ;$](img1502.png)
![$\displaystyle \left[ \hat{A},\hat{B}+\hat{C}\right]$](img1503.png)
![$\displaystyle \left[ \hat{A},\hat{B}\right]
+\left[ \hat{A},\hat{C}\right] ;$](img1504.png)
![$\displaystyle \left[ \hat{A},\hat{B}\hat{C}\right]$](img1505.png)
![$\displaystyle \left[ \hat{A},\hat{B}\right] \hat{C}
+\hat{B}\left[ \hat{A},\hat{C}\right] ;$](img1506.png)
![$\displaystyle \left[ \hat{A},\left[ \hat{B},\hat{C}\right] \right] +\left[ \hat...
...C},\hat{A}\right] \right] +\left[ \hat{C},\left[ \hat{B},\hat{A}\right]
\right]$](img1507.png)
![\begin{displaymath}
\left[ \hat{A},\hat{B}^{n}\right] =\sum_{s=0}^{n}\hat{B}^{s}\left[ \hat{A},
\hat{B}\right] \hat{B}^{n-s-1}.
\end{displaymath}](img1509.png)
![$\left[ \hat{A},f(\hat{B})\right] $](img1510.png) ausrechnen, falls
ausrechnen, falls ![\begin{eqnarray*}
\left[ \hat{l}_{x},\hat{l}_{y}\right] &=&i\hbar \hat{l}_{z} \\...
... \\
\left[ \hat{l}_{z},\hat{l}_{x}\right] &=&i\hbar \hat{l}_{y}
\end{eqnarray*}](img1512.png)
![\begin{eqnarray*}
\left[ \hat{l}_{z},\hat{l}_{x}^{2}\right] &=&i\hbar (\hat{l}_{...
...}\hat{l}_{y}) \\
\left[ \hat{l}_{z},\hat{l}_{z}^{2}\right] &=&0
\end{eqnarray*}](img1514.png)