



Next: Spezielle Operatoren
Up: Dualer Raum. Ket- und
Previous: Dualer Raum. Ket- und
Contents
Die Operatoren der Quantenmechanik können nun auch i.A. ohne Bezug auf
die Ortsdarstellung der Wellenfunktionen eingeführet werden. Ein
Operator  ordnet jedem Ket
ordnet jedem Ket
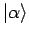 aus
seinem Definitionsbereich
aus
seinem Definitionsbereich 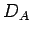 einen Ket
einen Ket
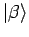 aus seinem Werteberiech zu:
aus seinem Werteberiech zu:
Zwei Operatoren 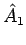 und
und 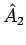 sind identisch, falls die
beiden den gleichen Definitionsbereich haben, und für jeden
sind identisch, falls die
beiden den gleichen Definitionsbereich haben, und für jeden
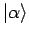 aus der Definitionsbereich gilt
aus der Definitionsbereich gilt
Der Identitätsoperator wir definiert durch
und der Null-Operator durch
Der Operator ist linear falls für jede
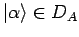 und
und
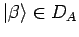 gilt:
gilt:
Die linearen Operatoren sind assoziativ und kommutativ gegenüber
der Addition, allerdings nicht kommutativ gegenüber der Multiplikation
(nacheinenderwirken).
- Der zu
 adjungierter Operator
adjungierter Operator 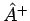
Eigenschaften:
- Seien
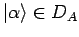 und
und
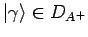 , so gilt:
, so gilt:
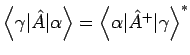 .
.
- Bei passendem Definitionsbereich
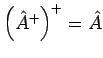 .
.
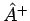 wirkt im dualen Raum
wirkt im dualen Raum 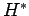 so wie
so wie  in
in 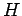 :
:
- Für das Produkt zweier Operatoren gilt:
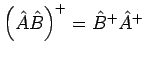 .
.
- Ein hermite'scher Operator:
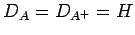 ,
,
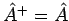 .
.




Next: Spezielle Operatoren
Up: Dualer Raum. Ket- und
Previous: Dualer Raum. Ket- und
Contents
Prof. Igor Sokolov
2005-02-14
![]() ordnet jedem Ket
ordnet jedem Ket
![]() aus
seinem Definitionsbereich
aus
seinem Definitionsbereich ![]() einen Ket
einen Ket
![]() aus seinem Werteberiech zu:
aus seinem Werteberiech zu:
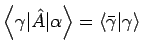 .
.
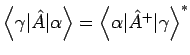 .
.
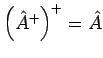 .
.
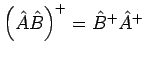 .
.