



Next: Zustandsvektoren und Operatoren als
Up: Dualer Raum. Ket- und
Previous: Die Lineare Operatoren
Contents
Hier führen wir die wichtigen Typen der Operatoren ein für weiteren
Gebrauch.
- Der inverse (oder reziproke) Operator: Für
einen Operator
 mit umkehrbar eindeutiger Abbildungsvorschrift
mit umkehrbar eindeutiger Abbildungsvorschrift
deren Definitions- und Wertebereiche zusammenfallen, kann ein inverser
Operator 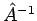 definiert werden, so dass
definiert werden, so dass
Es gilt:
Für die adjungierten Operatoren gilt:
- Der unitärer Operator:
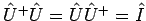 , d.h.
, d.h.
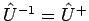 . Die unitäre Operatoren
ändern nicht das Skalarprodukt der Zustandsvektoren, und entsprechen der
Rotationen im Hilbertraum der Zustände: wenn
. Die unitäre Operatoren
ändern nicht das Skalarprodukt der Zustandsvektoren, und entsprechen der
Rotationen im Hilbertraum der Zustände: wenn
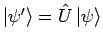 und
und
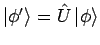 so gilt
so gilt
Die Änderung der Operatoren bei solcher Rotation ist wie folgt:
so dass
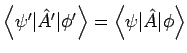 .
.
- Das dyadische Produkt: für
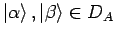 ist
ist
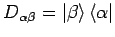 so definiert dass
so definiert dass
Der dazu adjungierte Operator
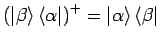 . Der Operator
. Der Operator
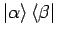 besitzt keine Inverse.
besitzt keine Inverse.
- Das diagonale dyadische Produkt
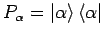 ist ein Projektionsoperator auf die Richtung
ist ein Projektionsoperator auf die Richtung
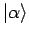 :
:
Eigenschaften:




Next: Zustandsvektoren und Operatoren als
Up: Dualer Raum. Ket- und
Previous: Die Lineare Operatoren
Contents
Prof. Igor Sokolov
2005-02-14
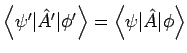 .
.
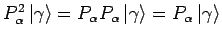 (idempotenz).
(idempotenz).
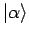 und
und
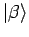 orthogonal sind, gilt:
orthogonal sind, gilt:
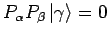 .
.