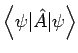 und die allg. Matrizenelemente
und die allg. Matrizenelemente
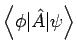 . Manchmal erweist es sich als zweckmäßig, dem
Symbol
. Manchmal erweist es sich als zweckmäßig, dem
Symbol
Der Zustand des Quantensystems wird durch den Zustandsvektor
![]() beschrieben. Die Skalarprodukte zweier Vektoren
beschrieben. Die Skalarprodukte zweier Vektoren
![]() sind (wenigstens in Ortsdarstellung)
definiert. Genau so sind auch die Mittelwerte
sind (wenigstens in Ortsdarstellung)
definiert. Genau so sind auch die Mittelwerte
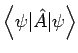 und die allg. Matrizenelemente
und die allg. Matrizenelemente
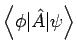 . Manchmal erweist es sich als zweckmäßig, dem
Symbol
. Manchmal erweist es sich als zweckmäßig, dem
Symbol
![]() eine eigenständige Bedeutung zu
geben.
eine eigenständige Bedeutung zu
geben.
Der eigentliche Zustandsvektor
![]() wird als
ket-Vektor (Ket) bezeichnet. Der Vektor
wird als
ket-Vektor (Ket) bezeichnet. Der Vektor
![]() (ein bra-Vektor, oder Bra) ist ein Element eines dualen Raumes. Die
Notation geht auf DIRAC zurück; ein Skalarprodukt aus Bra und
Ket ist einfach ein Bracket (Klammer).
(ein bra-Vektor, oder Bra) ist ein Element eines dualen Raumes. Die
Notation geht auf DIRAC zurück; ein Skalarprodukt aus Bra und
Ket ist einfach ein Bracket (Klammer).
In linearer Algebra kann man jedem linearen Vektorraum einen dualen Raum
gegenüberstellen. In einem linearen Raum gehört jede lineare Kombination (z.B.
![]() , wobei
, wobei
![]() und
und
![]() dem Raum angehören) wieder dem Raum an. Jede lineare Funktion
dem Raum angehören) wieder dem Raum an. Jede lineare Funktion
![]() , auf dem Raum der ket-Vektoren definiert,
ist ein Vektor des dualen Raums, und wird als entsprechende Bra
, auf dem Raum der ket-Vektoren definiert,
ist ein Vektor des dualen Raums, und wird als entsprechende Bra
![]() bezeichnet. Der Wert dieser Funktion, den sie
bei irgendeinem Vektor
bezeichnet. Der Wert dieser Funktion, den sie
bei irgendeinem Vektor
![]() annimmt ist eine komplexe
Zahl. Diese Zahl wird als
annimmt ist eine komplexe
Zahl. Diese Zahl wird als
![]() bezeichnet.
bezeichnet.
Ein Bra ist gleich 0,
![]() wenn für jede
wenn für jede
![]() ,
,
![]()
Zwei Bra
![]() und
und
![]() sind gleich wenn für jede
sind gleich wenn für jede
![]() ,
,
![]() .
.
Wenn der Raum von
![]() eine endliche Dimension hat,
dann hat der Raum der Bra-Vektoren die gleiche Dimension. Wenn der Raum von
eine endliche Dimension hat,
dann hat der Raum der Bra-Vektoren die gleiche Dimension. Wenn der Raum von
![]() unendlichdimensional ist, so ist es auch der Raum
von
unendlichdimensional ist, so ist es auch der Raum
von
![]() .
.
Es wird nngenommen, dass es eine Eins-zu-Eins-Entsprechung zwischen den
Vektoren der beiden Räume gibt: jedem Ket
![]() wird ein Bra
wird ein Bra
![]() gegenübergestellt, und
umgekehrt. Diese Entsprechung ist antilinear, d.h. dem ket-Vektor
gegenübergestellt, und
umgekehrt. Diese Entsprechung ist antilinear, d.h. dem ket-Vektor
![]() entspricht ein bra-Vektor
entspricht ein bra-Vektor
![]() .
.