



Next: Darstellungen der Quantenmechanik
Up: Zustandsvektoren und Operatoren als
Previous: Zustandsvektoren und Operatoren als
Contents
Betrachten wir nun einen unitären Operator 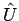 ,
,
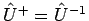 . Für diesen gilt
. Für diesen gilt
Die Zeilen und Spalten einer unitären Matrix sind orthonormiert:
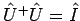
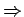
Betrachten wir jetzt irgendeinen Operator 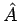 . Seien
. Seien
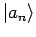 die Eigenfunktionen dieses Operators. In Basis
die Eigenfunktionen dieses Operators. In Basis
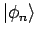 sind sie als Vektoren
sind sie als Vektoren
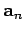 mit
Elementen
mit
Elementen
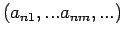 dargestellt,
dargestellt,
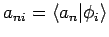 . Definieren wir nun eine Matrix
. Definieren wir nun eine Matrix
Die dazu adjungierte Matrix
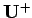 hat die Elemente
hat die Elemente
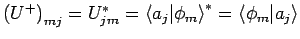 . Daher überzeugt man
sich, dass
. Daher überzeugt man
sich, dass 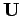 unitär ist:
unitär ist:
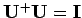 .
Betrachten wir nun eine Matrix
.
Betrachten wir nun eine Matrix
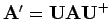 , mit
Elementen
, mit
Elementen
Die Matrix
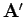 ist diagonal! Die unitäre
Transformation, die von der Matrix
ist diagonal! Die unitäre
Transformation, die von der Matrix 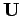 (Operator
(Operator 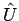 ) gegeben
ist, diagonalisiert
) gegeben
ist, diagonalisiert 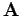 . Diese Transformation, auf die
Basisvektoren wirkend, transformiert die Basis
. Diese Transformation, auf die
Basisvektoren wirkend, transformiert die Basis
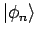 in der Basis der Eigenvektoren von
in der Basis der Eigenvektoren von 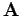 . I.A.
transformiert eine unitäre Transformation ein VONS der Basisvektoren in
das andere VONS von Basisvektoren.
. I.A.
transformiert eine unitäre Transformation ein VONS der Basisvektoren in
das andere VONS von Basisvektoren.
Bemerkung: Besteht die Basis auch aus uneigentlichen
Hilbert-Vektoren (kontinuierliches Spektrum) sollen die Summen durch die
Integrale ersetzt werden. Obwohl die Matrixdefinition inm eigentlichen Sinne
nicht mehr gilt, redet man trotzdem von Matrizenelementen u.s.w.
Die wichtigsten Eigenschaften der Matrizen bleiben dabei bestehen. Die
Elemente
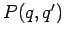 einer ''kontinuierlichen'' Matrix
einer ''kontinuierlichen'' Matrix
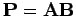 sind:
sind:
Es wird angenommen, dass die entsprechenden Integrale konvergieren. Die
Matrix ist diagonal falls
Nicht alle unendlichdimensionalen hermite'sche ''Matrizen'' können durch
eine unitäre Transformation diagonalisiert werden, i.e. besitzen einen
Spektrum. Wir nehmen aber an, dass alle Operatoren der Observablen
können diagonalisiert werden.
Für unendlichdimensionale Matrizen sind die linke und rechte Inverse
nicht unbedingt gleich: aus 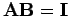 folgt nicht unbedingt
folgt nicht unbedingt
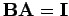 . Für die zueinander inversen Matrizen
. Für die zueinander inversen Matrizen 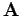 und
und 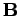 sollen die beiden Gleichungen gleichzeitig gelten.
sollen die beiden Gleichungen gleichzeitig gelten.
Im Falle des sowohl kontinuierlichen als auch diskreten Spektrums sind die
''Matrizen'' durch ein Gemisch aus kontinuierlichen und diskreten Indizes
numeriert.




Next: Darstellungen der Quantenmechanik
Up: Zustandsvektoren und Operatoren als
Previous: Zustandsvektoren und Operatoren als
Contents
Prof. Igor Sokolov
2005-02-14
![]() ,
,
![]() . Für diesen gilt
. Für diesen gilt
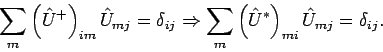

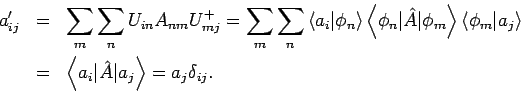
![]() einer ''kontinuierlichen'' Matrix
einer ''kontinuierlichen'' Matrix
![]() sind:
sind:
![]() folgt nicht unbedingt
folgt nicht unbedingt
![]() . Für die zueinander inversen Matrizen
. Für die zueinander inversen Matrizen ![]() und
und ![]() sollen die beiden Gleichungen gleichzeitig gelten.
sollen die beiden Gleichungen gleichzeitig gelten.