



Next: Unitäre Transformationen.
Up: Formalismus der Quantenmechanik und
Previous: Spezielle Operatoren
Contents
Die Zustandsvektoren (oder Ket-Vektoren
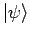 ) spannen
einen Hilbertraum
) spannen
einen Hilbertraum 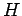 auf. Wir betrachten zunächst die Operatoren nur mit
diskretem Spektrum; die Funktionen
auf. Wir betrachten zunächst die Operatoren nur mit
diskretem Spektrum; die Funktionen
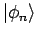 bilden
ein VONS der Funktionen. Jede
bilden
ein VONS der Funktionen. Jede
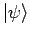 kann dann
folgendermassen dargestellt werden
kann dann
folgendermassen dargestellt werden
(das ist genau unsere
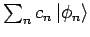 mit
mit
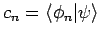 ). Eigentlich ist ein
Operator
). Eigentlich ist ein
Operator
ein Einheitsoperator in 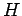 :
:
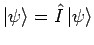 .
.
Der Funktion
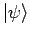 kann dann ein Spaltenvektor
gegenübergestellt werden:
kann dann ein Spaltenvektor
gegenübergestellt werden:
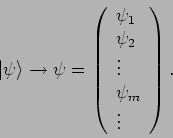 |
(42) |
(mit
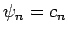 , das sind jetzt Zahlen, keine Funktionen).
Diese Spaltenvektoren erfüllen die Axiome eines
Hilbert-Raums, und können als Elementen veines Hilbert-Raums angesehen
werden.
, das sind jetzt Zahlen, keine Funktionen).
Diese Spaltenvektoren erfüllen die Axiome eines
Hilbert-Raums, und können als Elementen veines Hilbert-Raums angesehen
werden.
Betrachten wir nun einen auf die Funktion
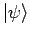 wirkenden Operator
wirkenden Operator  :
:
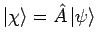 . Für
. Für  gilt:
gilt:
mit
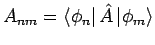 . Die
. Die 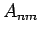 heissen die Matrizenelementen von
heissen die Matrizenelementen von  , die Werte von diesen sind durch die Festlegung der Basis
, die Werte von diesen sind durch die Festlegung der Basis
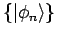 eindeutig festgelegt. Den ganzen Operator
kann man dann als Matrix schreiben:
eindeutig festgelegt. Den ganzen Operator
kann man dann als Matrix schreiben:
Wenn die Funktion
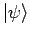 durch einen Vektor (42) dargestellt wird, so wird die Funktion
durch einen Vektor (42) dargestellt wird, so wird die Funktion
durch den Vektor mit Elementen
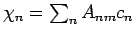 dargestellt:
dargestellt:
Subsections




Next: Unitäre Transformationen.
Up: Formalismus der Quantenmechanik und
Previous: Spezielle Operatoren
Contents
Prof. Igor Sokolov
2005-02-14
![]() ) spannen
einen Hilbertraum
) spannen
einen Hilbertraum ![]() auf. Wir betrachten zunächst die Operatoren nur mit
diskretem Spektrum; die Funktionen
auf. Wir betrachten zunächst die Operatoren nur mit
diskretem Spektrum; die Funktionen
![]() bilden
ein VONS der Funktionen. Jede
bilden
ein VONS der Funktionen. Jede
![]() kann dann
folgendermassen dargestellt werden
kann dann
folgendermassen dargestellt werden
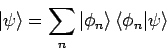
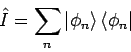
![]() kann dann ein Spaltenvektor
gegenübergestellt werden:
kann dann ein Spaltenvektor
gegenübergestellt werden:
![]() wirkenden Operator
wirkenden Operator ![]() :
:
![]() . Für
. Für ![]() gilt:
gilt:
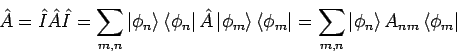

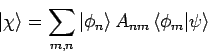
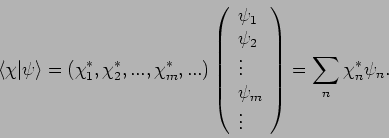
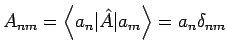 .
.