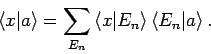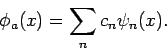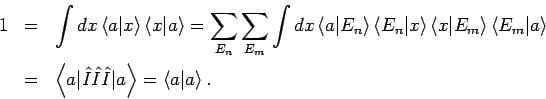Next: Die Impulsdarstellung
Up: Einige Darstellungen
Previous: Einige Darstellungen
Contents
Zur Darstellung des Zustandsvektors
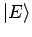 wählen wir
als Basisfunktionen nun die Eigenfunktionen eines Hamiltonoperators (wir
betrachten den Fall des diskreten Spektrums). In Ortsdarstellung bezeichnen
wir diese Funktionen mit
wählen wir
als Basisfunktionen nun die Eigenfunktionen eines Hamiltonoperators (wir
betrachten den Fall des diskreten Spektrums). In Ortsdarstellung bezeichnen
wir diese Funktionen mit
Für die konjungierten benutzen wir
Die Orthonormiertheit der EF kann man in der Form
oder
schreiben. Entwickeln wir die Funktionen der Ortsdarstellung des
Zustandsvektors
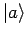 , d.h.
, d.h.
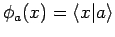 , so bekommen wir
, so bekommen wir
Der 1. Multiplikator ist nichts anderes als
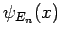 , und der
Zweite nichtd anders als der Entwicklungskoeffizient von Zustand
, und der
Zweite nichtd anders als der Entwicklungskoeffizient von Zustand
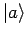 in der VONS von Eigenfunktionen von
in der VONS von Eigenfunktionen von 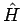 (in
gewöhnlicher Schreibweise sollte man statt
(in
gewöhnlicher Schreibweise sollte man statt
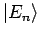 eigentlich
eigentlich
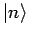 schreiben, und über
schreiben, und über 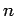 summieren;
die jetzige Schreibweise unterstreicht dass
summieren;
die jetzige Schreibweise unterstreicht dass 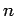 eigentlich die mögliche
Energien der Eigenzuständen numeriert). Diese ist nichts anders als
unsere vorherige Entwicklung
eigentlich die mögliche
Energien der Eigenzuständen numeriert). Diese ist nichts anders als
unsere vorherige Entwicklung
Das Skalarprodukt
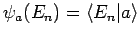 fassen wir als die Wellenfunktion des Zustandes
fassen wir als die Wellenfunktion des Zustandes
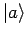 in
der Energiedarstellung auf. Die unabhängige Veränderliche der
Wellenfunktion in Energiedarstellung
in
der Energiedarstellung auf. Die unabhängige Veränderliche der
Wellenfunktion in Energiedarstellung 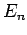 ist diskret, es ist die Energie
des Systems, und das Betragsquadrat der WF in der Energiedarstellung
ist diskret, es ist die Energie
des Systems, und das Betragsquadrat der WF in der Energiedarstellung
ist die Wahrscheinlichkeit, bei der Messung der Energie in dem Zustand
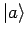 den Wert
den Wert 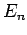 zu bekommen. Waren die Funktionen
in Ortsdarstellung normiert, so sind sie es in der Energiedarstellung auch:
Stellt man die Definitionen
zu bekommen. Waren die Funktionen
in Ortsdarstellung normiert, so sind sie es in der Energiedarstellung auch:
Stellt man die Definitionen
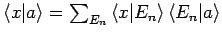 und
und
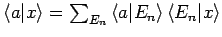 in der Normierungsbedingung für
Koordinatendarstellung
in der Normierungsbedingung für
Koordinatendarstellung
ein, so erhält man




Next: Die Impulsdarstellung
Up: Einige Darstellungen
Previous: Einige Darstellungen
Contents
Prof. Igor Sokolov
2005-02-14
![]() wählen wir
als Basisfunktionen nun die Eigenfunktionen eines Hamiltonoperators (wir
betrachten den Fall des diskreten Spektrums). In Ortsdarstellung bezeichnen
wir diese Funktionen mit
wählen wir
als Basisfunktionen nun die Eigenfunktionen eines Hamiltonoperators (wir
betrachten den Fall des diskreten Spektrums). In Ortsdarstellung bezeichnen
wir diese Funktionen mit