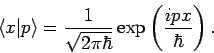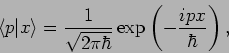Next: Darstellungen der Operatoren
Up: Einige Darstellungen
Previous: Die Energiedarstellung.
Contents
Impuls, wie Koordinate auch, entspricht einem Operator mit kontinuierlichen
Spektrum. In der Impulsdarstellung (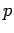 -Darstellung) sind die
Basisfunktionen die Eigenfkt. von Impulsoperator
-Darstellung) sind die
Basisfunktionen die Eigenfkt. von Impulsoperator
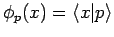 . Sie sind orthonormiert
. Sie sind orthonormiert
Wir entwickeln die Wellenfunktion
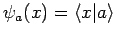 des Zustandes
des Zustandes
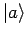 nach VONS der EF
von
nach VONS der EF
von 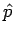 :
:
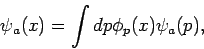 |
(44) |
oder
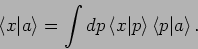 |
(45) |
Die Funktionen
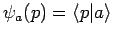 bestimmen den
Zustandsvektor in
bestimmen den
Zustandsvektor in 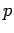 -Darstellung. Das Betragsquadrat dieser Funktion ist
die Wahrscheinlichkeitsdichte im Impulsraum:
-Darstellung. Das Betragsquadrat dieser Funktion ist
die Wahrscheinlichkeitsdichte im Impulsraum:
Die inverse Transformation lautet
Die EF des Impulsoperators in Ortsdarstellung sind explizit bekannt:
Die Fkt. der inversen Transformation lautet dann
das ist die EF des Ortes in Impulsdarstellung.
Prof. Igor Sokolov
2005-02-14
![]() -Darstellung) sind die
Basisfunktionen die Eigenfkt. von Impulsoperator
-Darstellung) sind die
Basisfunktionen die Eigenfkt. von Impulsoperator
![]() . Sie sind orthonormiert
. Sie sind orthonormiert