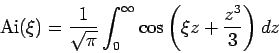Next: Bemerkungen:
Up: Darstellungen der Quantenmechanik
Previous: Darstellungen der Operatoren
Contents
Der Hamiltonian in Ortsdarstellung
geht in Impulsdarstellung in
über. In Matrixschreibweise bekommen wir
oder
Der Operator
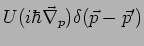 ist eigentlich ein Integraloperator:
ist eigentlich ein Integraloperator:
Führen wir die Fouriertransformierte
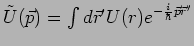 ein, so erhalten wir
ein, so erhalten wir
Die Schrödingergleichung
in Impulsdarstellung nimmt demnach die Form der integro-differentialen Gl.
oder
an. Das ist eigentlich nichts anders als die Fouriertransformierte der
Schrödinger Gl. der Ortsdarstellung.
Beispiel: 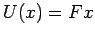 . Dieses lineare Potential haben wir bei der
Herleitung der WKB-Näherung ( 6.1) benutzt. Wie sieht die entsprechende
Eigenfunktion (eigenwert 0!) aus? In Ortsdarstellung
. Dieses lineare Potential haben wir bei der
Herleitung der WKB-Näherung ( 6.1) benutzt. Wie sieht die entsprechende
Eigenfunktion (eigenwert 0!) aus? In Ortsdarstellung
In Impulsdarstellung:
diese Gl. ist definitiv einfacher. Die Lösung kann man sofort
aufschreiben:
Daher
Setzen wir
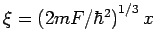 , so sehen wir dass
, so sehen wir dass
mit
die Airy-Funktion ist (das ist ihre Definition!).
Subsections




Next: Bemerkungen:
Up: Darstellungen der Quantenmechanik
Previous: Darstellungen der Operatoren
Contents
Prof. Igor Sokolov
2005-02-14
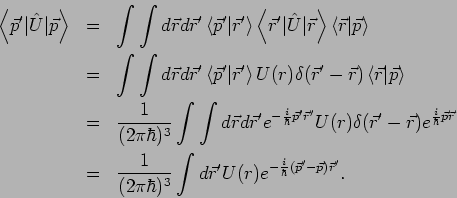
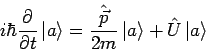
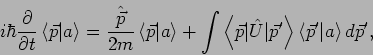
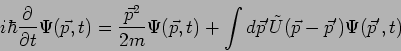
![]() . Dieses lineare Potential haben wir bei der
Herleitung der WKB-Näherung ( 6.1) benutzt. Wie sieht die entsprechende
Eigenfunktion (eigenwert 0!) aus? In Ortsdarstellung
. Dieses lineare Potential haben wir bei der
Herleitung der WKB-Näherung ( 6.1) benutzt. Wie sieht die entsprechende
Eigenfunktion (eigenwert 0!) aus? In Ortsdarstellung
![\begin{displaymath}
\left[ -\frac{\hbar ^{2}}{2m}\frac{d^{2}}{dx^{2}}+Fx\right] \psi (x)=0.
\end{displaymath}](img1747.png)
![\begin{displaymath}
\left[ \frac{p^{2}}{2m}+F\frac{d}{dp}\right] \psi (p)=0,
\end{displaymath}](img1748.png)
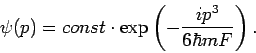
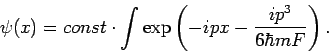
![\begin{displaymath}
\psi (\xi )\propto \int \exp \left[ -i\left( \xi z-\frac{z^{3}}{3}\right)
\right] dz=2\sqrt{\pi }\mathrm{Ai}(\xi ),
\end{displaymath}](img1752.png)