



Next: Beispiel: Schrödinger-Gl. in Impulsdarstellung
Up: Einige Darstellungen
Previous: Die Impulsdarstellung
Contents
In der Ortsdarstellung sind die Operatoren Funktionen der Koordinaten und
der Ableitungen nach den Koordinaten. Wendet man diese auf Funktionen in
Ortsdarstellung an, so ergeben sich andere Funktionen in Ortsdarstellung:
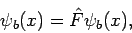 |
(46) |
oder
Anhand von Gl.(43) wird 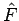 in Energiedarstellung
durch eine Matrix
in Energiedarstellung
durch eine Matrix 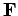 gegeben:
gegeben:
Betrachten wir den Hamiltonoperator 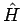 in der Energiedarstellung, so
entspricht dieser einer diagonalen Matrix:
in der Energiedarstellung, so
entspricht dieser einer diagonalen Matrix:
Betrachten wir nun die Gestalt von 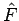 in Impulsdarstellung.
Dafür benutzen wir die Entwicklungen der Eigenfunktionen des Ortes in
Impulsdarstellung, Gl'en (44,45). Die Gl.(43) ergibt
dann
in Impulsdarstellung.
Dafür benutzen wir die Entwicklungen der Eigenfunktionen des Ortes in
Impulsdarstellung, Gl'en (44,45). Die Gl.(43) ergibt
dann
Die Operatoren in Ortsdarstellung sind normalerweise lokal, d.h.
die Werte des unabhängigen Variablen auf beiden Seiten der Gl.(46
sind gleich: diese Operatoren sind daher diagonal in der Koordinatendarstellung,
so dass wir eigentlich nur 1 Integral benötigen:
Betrachten wir nun diese Situation explizit. In Ortsdarstellung ist der
Impulsoperator
Im Impulsdarstellung daher gilt:
Die Gestalt des Ortsoperator in der Impilsdarstellung ergibt sich aus
mit
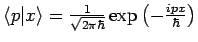 . Daher
. Daher
(Nachprüfen durch partielle Integration!). Demnach entspricht die
Koordinate in Impulsdarstellung einem Differentialoperator
Man überzeige sich direkt, dass obwohl die Gestalt der Operatoren von
der Darstellung abhängt, die Kommutationseigenschaft
sowohl in Orts- als auch in Impulsdarstellung gilt. Für den
dreidimensionalen Fall gilt:
(der Gradient im Impulsraum wird als
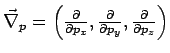 definiert). Mittels dieser Gl. kann man in
definiert). Mittels dieser Gl. kann man in 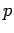 -Darstellung
die explizite Gestalt der Operatoren der Physikalischen Größen
aufschreiben, die in der klassischen Physik der Funktionen der Koordinaten
und Impulse entsprechen.
-Darstellung
die explizite Gestalt der Operatoren der Physikalischen Größen
aufschreiben, die in der klassischen Physik der Funktionen der Koordinaten
und Impulse entsprechen.




Next: Beispiel: Schrödinger-Gl. in Impulsdarstellung
Up: Einige Darstellungen
Previous: Die Impulsdarstellung
Contents
Prof. Igor Sokolov
2005-02-14
![\begin{eqnarray*}
\left\langle p^{\prime }\vert\hat{p}\vert p\right\rangle &=&-\...
...p-p^{\prime }\right) x}{\hbar }\right]
=p\delta (p^{\prime }-p).
\end{eqnarray*}](img1727.png)
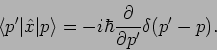
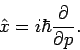
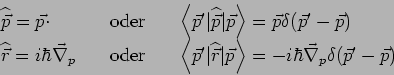
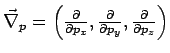 definiert). Mittels dieser Gl. kann man in
definiert). Mittels dieser Gl. kann man in