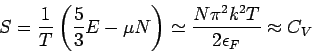Nächste Seite: Das ideale Bose-Gas
Aufwärts: Das ideale Fermi-Gas
Vorherige Seite: Maximale Entartung ()
Das Verhalten von
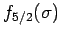 und
und
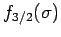 für
für 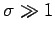 lautet
lautet
und
Aus
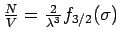 folgt dann:
folgt dann:
Damit folgt
Die spezifische Wärme
strebt gegen 0 für
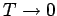 (3. Hauptzstz!).
(3. Hauptzstz!).
Die thermische Zustandsgleichung lautet:
Die Entropie
strebt gegen 0 für
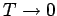 (3. HS).
(3. HS).
Anwendungen bezüglich der Leitungselektronen in Metallen: siehe
Hausaufgaben.
Prof. Igor Sokolov
2004-07-01
![]() und
und
![]() für
für ![]() lautet
lautet
![\begin{displaymath}
f_{5/2}(\sigma )=\frac{4}{\sqrt{\pi }}\int_{0}^{\infty }dx\,...
...+\frac{5\pi ^{2}}{8\left( \ln \sigma \right) ^{2}}+...\right]
\end{displaymath}](img367.png)
![\begin{displaymath}
f_{3/2}(\sigma )=\sigma \frac{d}{d\sigma }f_{5/2}(\sigma )\s...
...%
\frac{\pi ^{2}}{8\left( \ln \sigma \right) ^{2}}+...\right]
\end{displaymath}](img368.png)
![\begin{displaymath}
\frac{\mu }{kT}=\ln \sigma \simeq \frac{\epsilon _{F}}{\kapp...
...}}{12}\left( \frac{kT}{\epsilon _{F}}\right) ^{2}+...\right] .
\end{displaymath}](img370.png)
![\begin{displaymath}
E=\frac{3kTV}{\lambda ^{3}}f_{5/2}(\sigma )\simeq \frac{3}{5...
...}}{12}\left( \frac{kT}{\epsilon _{F}}\right)
^{2}+...\right] .
\end{displaymath}](img371.png)
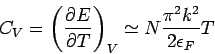
![\begin{displaymath}
p=\frac{2E}{3V}={\underbrace{\frac{2}{5}%
\frac{N}{V}\epsilo...
...}{12}\left( \frac{kT}{%
\epsilon _{F}}\right) ^{2}+...\right]
\end{displaymath}](img373.png)