


Nächste Seite: Die Kompressibilitätsgleichung
Aufwärts: Die Paarverteilungsfunktion und die
Vorherige Seite: Die Paarverteilungsfunktion und die
Die potentielle Energie ist eine Summe über die Paarwechselwirkungen 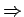
Betrachten wir jetzt ein Integral
für eine beliebige Funktion der Koordinaten 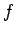 . Nehmen wir an, dass
die Funktion
. Nehmen wir an, dass
die Funktion 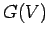 nur vom Volumen (und nicht von der Form des Systems)
abhängt. Betrachten wir eine isotrope Ausdehnung des Systems, wodurch
alle räumliche Abmessungen des Systems um den Faktor
nur vom Volumen (und nicht von der Form des Systems)
abhängt. Betrachten wir eine isotrope Ausdehnung des Systems, wodurch
alle räumliche Abmessungen des Systems um den Faktor 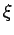 grösser
geworden sind, und das Volumen hat sich um Faktor
grösser
geworden sind, und das Volumen hat sich um Faktor 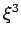 verändert.
Es gilt i.A.
verändert.
Es gilt i.A.
Am Ende nehmen wir 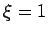 . Die Funktion
. Die Funktion 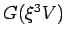 kann durch 2
äquivalente Ausdrucke dargestellt werden
kann durch 2
äquivalente Ausdrucke dargestellt werden
(Variablenwechsel!). In unserem Fall bedeutet das, dass
(dieser Trick stammt von BOGOLYUBOV) 
und insgesamt
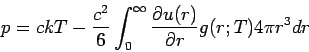 |
(17) |
mit 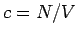 . Gl. (17) ist eine absolut allgemeine Form der
Zustandsgleichung eines Fluids. Man kann z.B.
. Gl. (17) ist eine absolut allgemeine Form der
Zustandsgleichung eines Fluids. Man kann z.B. 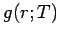 aus Simulationen
direkt erhalten, und dann
aus Simulationen
direkt erhalten, und dann 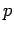 berechnen.
berechnen.
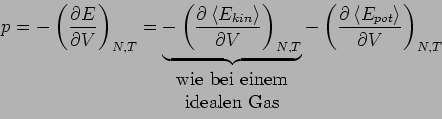
Zusammenhang mit dem 2. Virialkoeffizient: Da für ein verdünntes Gas
nur die Paarwechselwirkungen eine Rolle spielen, gilt:
(ein Boltzmannfaktor). In dieser Näherung
so dass
Hausaufgabe: Zeigen Sie das dieser Ausdruck mit unserer Definition, Gl. (15) identisch ist!



Nächste Seite: Die Kompressibilitätsgleichung
Aufwärts: Die Paarverteilungsfunktion und die
Vorherige Seite: Die Paarverteilungsfunktion und die
Prof. Igor Sokolov
2004-07-01

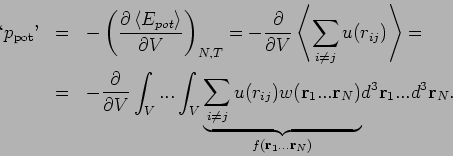
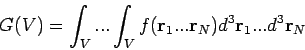
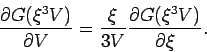
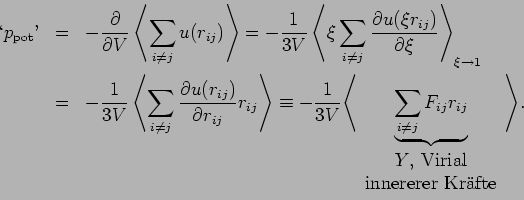
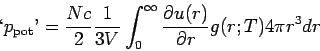
![\begin{displaymath}
\lim_{c\rightarrow 0}g(r;T)=\exp \left[ -\frac{u(r)}{kT}\right]
\end{displaymath}](img626.png)
![\begin{displaymath}
\frac{pV}{NkT}=1-c\frac{1}{6kT}\int_{0}^{\infty }\frac{\part...
...{%
\partial r}\exp \left[ -\frac{u(r)}{kT}\right] 4\pi r^{3}dr
\end{displaymath}](img627.png)
![\begin{displaymath}
B_{2}=-\frac{1}{6kT}\int_{0}^{\infty }\frac{\partial u(r)}{\partial r}\exp
\left[ -\frac{u(r)}{kT}\right] 4\pi r^{3}dr.
\end{displaymath}](img628.png)