


Nächste Seite: Die Mikrokanonische Gesamtheit
Aufwärts: Die Kanonische Zustandssumme
Vorherige Seite: Vibration
Das ist ein zu den vorherigen sehr nah verwandtes Modell, wo die
Schwingungen der Atome in einem Kristallgitter durch 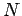 unabhängigen
3-dimensionalen Oszillatoren gleicher Frequenz
unabhängigen
3-dimensionalen Oszillatoren gleicher Frequenz 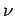 beschrieben werden
(insgesamt
beschrieben werden
(insgesamt 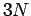 unabhängigen Schwingungsmoden gleicher Frequenz, so dass
unabhängigen Schwingungsmoden gleicher Frequenz, so dass
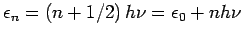 . Pro Mode:
. Pro Mode:
so dass
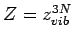 und
und
(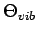 wird in diesem Zusammenhang oft Einstein-Temperatur
genannt; die Beziehung für
wird in diesem Zusammenhang oft Einstein-Temperatur
genannt; die Beziehung für
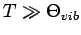 wird als
Dulong-Petit-Gesetz bezeichnet).
wird als
Dulong-Petit-Gesetz bezeichnet).
Die Abnahme von 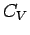 für
für
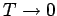 ist zwar im Einklang mit
dem 3. Hauptsatz, ist aber (verglichen mit Experimenten) zu schnell. Abhilfe
wurde vom Debye-Modell geliefert, das die Frequenzunterschede der
Eigenmoden der Schwingungen in Betraht nimmt (später).
ist zwar im Einklang mit
dem 3. Hauptsatz, ist aber (verglichen mit Experimenten) zu schnell. Abhilfe
wurde vom Debye-Modell geliefert, das die Frequenzunterschede der
Eigenmoden der Schwingungen in Betraht nimmt (später).
Prof. Igor Sokolov
2004-07-01
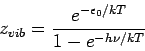
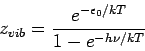
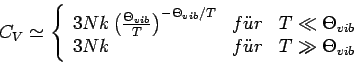
![]() für
für
![]() ist zwar im Einklang mit
dem 3. Hauptsatz, ist aber (verglichen mit Experimenten) zu schnell. Abhilfe
wurde vom Debye-Modell geliefert, das die Frequenzunterschede der
Eigenmoden der Schwingungen in Betraht nimmt (später).
ist zwar im Einklang mit
dem 3. Hauptsatz, ist aber (verglichen mit Experimenten) zu schnell. Abhilfe
wurde vom Debye-Modell geliefert, das die Frequenzunterschede der
Eigenmoden der Schwingungen in Betraht nimmt (später).