Arthur Straube

Recent highlights

A novel two-variable model of a pH oscillor in an open reactor

Background & motivation: We study an urea-urease-based pH oscillator confined to a lipid vesicle that serves as an open reactor. In contrast to conventional pH oscillators in closed reactors, the exchange with the vesicle exterior periodically resets the pH clock that switches the system from acid to basic, resulting in self-sustained oscillations. We analyze the structure of the limit cycle, which controls the dynamics for giant vesicles and dominates the strongly stochastic oscillations in small vesicles of submicrometer size. We derive reduced two-variable models, amenable to analytic treatments, and show that the accuracy of predictions, including the period of oscillations, is highly sensitive to the choice of the reduction scheme. The accurate description of a single pH oscillator is crucial for rationalizing experiments and understanding communication of vesicles and synchronization of rhythms.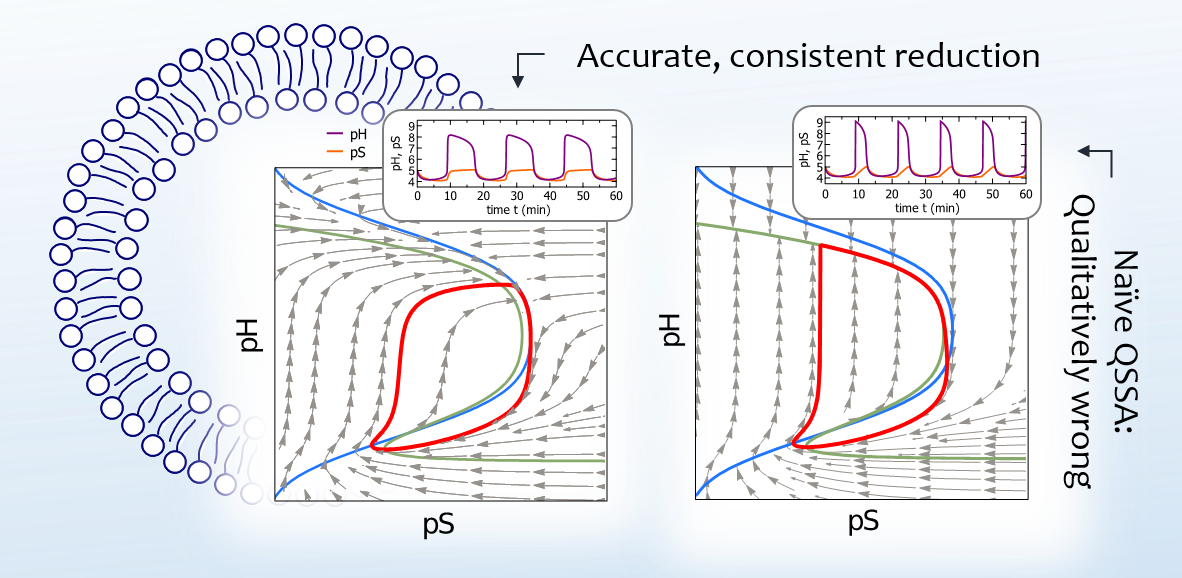


Figure: The unilamellar vesicle membrane as an open reactor (schematic). Phase flows from a virtually exact (left) and a naively reduced (right) models. Although the nullclines (green and blue lines) are identical, the phase flows are qualitatively different. The nature of the limit cycle (red line) is eventually determined by the blue nullcline (not the green nullcline, accompanied by degeneracy in the flow field at its upper branch), which is captured correctly only via the properly reduced model. Therefore, the accuracy of the amplitude and period of oscillations are highly sensitive to the choice of the reduction scheme.

Findings: Starting from a four-variable model, we have reduced it to a new very accurate two-variable model. Exclusion of one product variable appears highly accurate within a standard quasi-steady state approximation (QSSA). The latter presents a constraint that is in contradiction with the similar QSSA for another product variable. Instead, we suggest a virtually exact solution resulting in a simple two-variable model. In particular, we further show that: i) the constraint explains why the structure of limit cycle is best unveiled in terms of logarithmic scales, in contrast to conventional models; ii) the naive QSSA elimination of variables results in degenerate behavior in the base part of the phase plane and predicts a qualitatively incorrect formation of the limit cycle; iii) explicit account of water ionization is unimportant for oscillation dynamics. Finally, we have performed a stability analysis that determines existence of oscillatory regimes for experimentally relvant parameters.

Publication:
A.V. Straube, S. Winkelmann, F. Höfling,
Accurate reduced models for the pH oscillations in the urea−urease reaction confined to giant lipid vesicles, J. Phys. Chem. B 127, 2955 (2023) [arXiv:2212.14503]