Rechenbeispiel 2: Abschätzung der Bindungsenergie der negativen molekularen Wasserstoffions $\mathrm{H}_{2}^{-}$.

Nachdem wir dieses einfache Beispiel betrachtet haben, können wir es auf eine physikalisch relevante Situation anwenden. Betrachten wir das System aus 2 Protonen (sie sind so schwer, dass wir sie als praktisch unbewegliche klassische Teilchen betrachten können) und einem Elektron (der zuerst in einem Grundzustand des Wasserstoffatoms auf einem davon lokalisiert war). Das Potential (Atomeinheiten!) lautet

$$U(r)=-\frac{1}{r_{1}}-\frac{1}{r_{2}}$$

wobei $r_{1,2}$ die Abstände des Elektrons von 1. bzw. 2. Kern sind. Wir wählen die $x$-Achse so, dass sie durch die Kerne geht (einer davon in Koordinatenanfang, der andere bei $x=R$). Die WF'nen der ungestörten Zustände $\left\vert L\right\rangle$ und $\left\vert R\right\rangle$ (alle andere Zustände sind in der Energie weit genug entfernt):

$$\begin{eqnarray*} \psi _{L}(\mathbf{r}) &=&\frac{1}{\sqrt{\pi }}e^{-r}, \\ \psi... ...}{\sqrt{\pi }}e^{-\left\vert \mathbf{r}-\mathbf{R}\right\vert }. \end{eqnarray*}$$

(beide sind 1s-Zustände; es sind die vollständigen WF angegeben, nicht nur die radiale Teile, wie in der VL5)

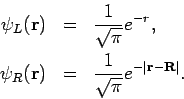
Die Matrizenelemente sind:

$$H_{11}=H_{22}=E_{0}-\int \left\vert \psi _{L}(\mathbf{r})\right\vert ^{2}\frac{1}{% r_{2}}d\mathbf{r}$$

und

$$H_{12}=-\int \psi _{L}(\mathbf{r})\psi _{R}(\mathbf{r})\frac{1}{r_{2}}d\mathbf{r}$$

In Polarkoordinaten

$$H_{11}=-2\int e^{-2r}\frac{1}{\sqrt{R^{2}-2rR\xi +r^{2}}}r^{2}drd\xi$$

und

$$H_{12}=-2\int e^{-r}e^{-\sqrt{R^{2}-2rR\xi +r^{2}}}\frac{1}{\sqrt{% R^{2}-2rR\xi +r^{2}}}r^{2}drd\xi$$

(mit $\xi =\cos \theta$). Der Grunszustand entspricht der Energie $E_{-}$.

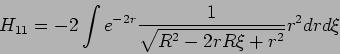
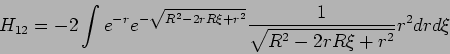
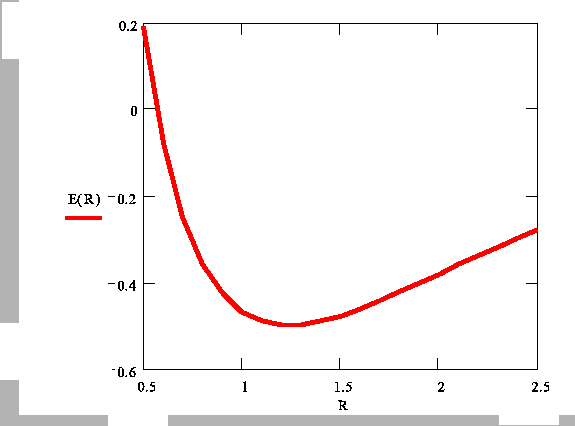
Die Erniedrigung der Energie des elektronischen Zuständen bei kleineren $% R$ entspricht dem Wachstum der Energie der Coulomb-Abstoßung zwischen den Kernen, so dass der Gleichgewichtsabstand zwischen den Kernen in etwa dem Minimum der $E(R)=E_{-}(R)+1/R$ entspricht. Die entsprechende Kurve sieht wie folgt aus: