



Next: Störungstheorie in stationären Zuständen
Up: Quantenmechanik I WS 04/05
Previous: Wechselwirkungsbild.
Contents
Oft ist der Hamiltonian eines Systems als eine Summe
darstellbar, wobei der Hamiltonian 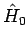 in gewissem Sinne
''einfach'' ist, so dass sein Spektrum und seine Eigenfunktionen bekannt sind. In
vielen solchen Fällen kan mann das Spektrum und die EF des
Gesamthamiltonians
in gewissem Sinne
''einfach'' ist, so dass sein Spektrum und seine Eigenfunktionen bekannt sind. In
vielen solchen Fällen kan mann das Spektrum und die EF des
Gesamthamiltonians 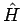 näherungsweise mit Hilfe der
Störungstheorie bestimmen. Hierbei bezeichnen wir das System, das durch
den Hamiltonian
näherungsweise mit Hilfe der
Störungstheorie bestimmen. Hierbei bezeichnen wir das System, das durch
den Hamiltonian 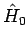 beschrieben wird, als ''ungestörtes System'',
und
beschrieben wird, als ''ungestörtes System'',
und 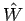 als ''Störung''.
als ''Störung''.
Die Störung wird mit Hilfe eines formalen reelen Parameters 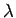 (Koppelkonstante) eingeschaltet:
(Koppelkonstante) eingeschaltet:
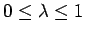 . Es wird angenommen dass für
. Es wird angenommen dass für
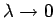 die Eigenwerte
die Eigenwerte 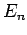 und die Eigenfunktionen
und die Eigenfunktionen
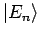 des System in die entsprechenden Eigenwerte
des System in die entsprechenden Eigenwerte 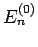 und
Eigenfunktionen
und
Eigenfunktionen
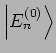 des ungestörten
Problems übergehen. Der formale Trick besteht darin, die Entwicklungen
nach Potenzen von
des ungestörten
Problems übergehen. Der formale Trick besteht darin, die Entwicklungen
nach Potenzen von 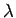 zu betrachten, und dann
zu betrachten, und dann 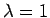 zu setzen.
zu setzen.
Subsections
Prof. Igor Sokolov
2005-02-14
![]() (Koppelkonstante) eingeschaltet:
(Koppelkonstante) eingeschaltet:
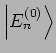 des ungestörten
Problems übergehen. Der formale Trick besteht darin, die Entwicklungen
nach Potenzen von
des ungestörten
Problems übergehen. Der formale Trick besteht darin, die Entwicklungen
nach Potenzen von