



Next: Statistische Interpretation der Wellenfunktion
Up: Beispiel: Das Rechteckpotential.
Previous: Spezialfall: Das -Potential.
Contents
Wenn 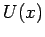 symmetrisch in bezug auf
symmetrisch in bezug auf 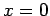 ist, dann
ist, dann 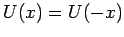 . Die SGl.
ändert sich nicht, wenn man von
. Die SGl.
ändert sich nicht, wenn man von 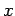 zu
zu 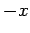 wechselt (sowohl
wechselt (sowohl
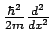 als auch
als auch 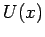 ändern sich
nicht). D.h.wenn
ändern sich
nicht). D.h.wenn
eine Eigenfunktion (EF) ist, dann ist
auch eine EF. Wegen der Linearität ist auch die gerade Fkt.
und die ungerade Fkt.
(wenn sie nicht verschwinden) die Ls'gen.




Next: Statistische Interpretation der Wellenfunktion
Up: Beispiel: Das Rechteckpotential.
Previous: Spezialfall: Das -Potential.
Contents
Prof. Igor Sokolov
2005-02-14
![]() symmetrisch in bezug auf
symmetrisch in bezug auf ![]() ist, dann
ist, dann ![]() . Die SGl.
ändert sich nicht, wenn man von
. Die SGl.
ändert sich nicht, wenn man von ![]() zu
zu ![]() wechselt (sowohl
wechselt (sowohl
![]() als auch
als auch ![]() ändern sich
nicht). D.h.wenn
ändern sich
nicht). D.h.wenn