



Next: Quasiklassische Näherung (WKB-Näherung)
Up: Quantenmechanik I WS 04/05
Previous: Teilchen im Magnetfeld.
Contents
In hinreichend stetigen äußeren Feldern und für grosse Impulse
des Teilchens (kleine de-Broglie-Wellenlänge) unterscheidet sich das
Verhalten des Teilchens nur wenig von den klassischen Vorhersagen. Wir
untersuchen jetzt den Übergang von der klassischen Mechanik zur
Quantenmechanik, der formal dem Übergang von der Wellenoptik zur
geometrischen Optik analog ist. Wir konzentrieren uns auf die Situation ohne
Magnetfeld.
Man kann der Grenzübergang von der Quantenmechanik zur klassischen
Mechanik am einfachsten untersuchen, wenn man der Wellenfunktion in der form
darstellt. Einsetzen in die Schrödinger-Gleichung
ergibt für
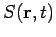
Vergleichen wir das mit der Hamilton-Jakobischen Gleichung der klassischen
Mechanik
mit der klassischen Wirkungsfunktion
so sehen wir dass die letzte den Grenzfall der ersten mit
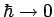 darstellt.
darstellt.
(Zur Erinnerung: Die Bahnkurven des klassischen Teilchens sind normal zu
Flächen 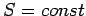 : Da
: Da
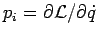 bekommt man
bekommt man
(die Bewegungsgl.) und
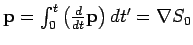 . Im einfachsten Fall
. Im einfachsten Fall
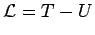 ,
ist somit die HJ-Gleichung eine Identität
,
ist somit die HJ-Gleichung eine Identität 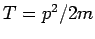 ).
).
Wir wollen feststellen, wann eine klassischen Beschreibung möglich ist.
Wir konzentrieren uns auf stationäre Zustände. Daher
Die Zeitabhängigkeit spaltet sich ab:
Dabei bekommen wir
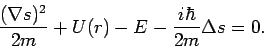 |
(18) |
Der Übergang zur klassischen Mechanik erfolgt durch
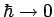 :
:
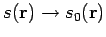 :
:
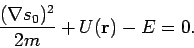 |
(19) |
Die Funktion
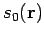 ist mit dem Impuls des Teilchen durch
ist mit dem Impuls des Teilchen durch
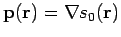 verbunden. Die Näherung
von Gl.(18) durch die Gl.(19) ist dann möglich wenn das
letzte Glied klein ist im Vergleich mit dem ersten:
verbunden. Die Näherung
von Gl.(18) durch die Gl.(19) ist dann möglich wenn das
letzte Glied klein ist im Vergleich mit dem ersten:
i.e. wenn
Im Spezialfall eindimensionaler Bewegung wird aus der Ungleichung
Unter Verwendung von
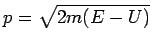 kann man diese Ungleichung auch in
anderer Form schreiben:
kann man diese Ungleichung auch in
anderer Form schreiben:
Daraus folgt, dass wir ein quantenmechanischen System genähert klassisch
behandeln können wenn die Teilchen große Impulse besitzen und sich in
einem Feld mit kleinen Gradienten bewegen.
Wenn wir 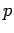 durch die de-Broglie-Wellenlänge ausdrucken, bekommen wir
durch die de-Broglie-Wellenlänge ausdrucken, bekommen wir
Die Änderung der Wellenlänge auf der Strecke 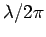 muß sehr klein gegenüber der Wellenlänge sein. Ist die Abmessung des
Systems
muß sehr klein gegenüber der Wellenlänge sein. Ist die Abmessung des
Systems 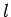 , so gilt
, so gilt
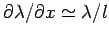 :
:
Subsections




Next: Quasiklassische Näherung (WKB-Näherung)
Up: Quantenmechanik I WS 04/05
Previous: Teilchen im Magnetfeld.
Contents
Prof. Igor Sokolov
2005-02-14
![\begin{displaymath}
\Psi (\mathbf{r},t)=\exp \left[ \frac{i}{\hbar }S(\mathbf{r},t)\right]
\end{displaymath}](img848.png)
![\begin{displaymath}
\Psi (\mathbf{r},t)=\exp \left[ \frac{i}{\hbar }S(\mathbf{r},t)\right]
\end{displaymath}](img848.png)
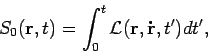
![]() : Da
: Da
![]() bekommt man
bekommt man
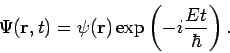
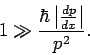
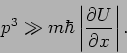
![]() durch die de-Broglie-Wellenlänge ausdrucken, bekommen wir
durch die de-Broglie-Wellenlänge ausdrucken, bekommen wir